Problema 1 
Escribir algebraicamente las siguientes expresiones:
- El doble de un número \(x\).
- El triple de un número \(x\).
- El doble de un número \(x\) más 5.
- El cuadrado del triple de un número \(x\).
- Las tres cuartas partes de un número \(x\).
SOLUCIÓN:
El doble de un número se obtiene multiplicándolo por 2, por tanto, el doble de \(x\) es \(2x\).
El triple de un número se obtiene multiplicándolo por 3, por tanto, el triple de \(x\) es \(3x\).
El doble de \(x\) es \(2x\), por tanto, si le sumamos 5, tenemos \(2x+5\)
El triple de \(x\) es \(3x\), así que su cuadrado es
$$ (3x)^2 = 3^2 \cdot x^2 = 9x^2 $$
Nota: hemos usado la propiedad de la potencia "la potencia de un producto es el producto de las potencias".
La cuarta parte de \(x\) es
$$ \frac{1}{4} \cdot x = \frac{x}{4}$$
Por tanto, tres cuartas partes de \(x\) son
$$ 3\cdot \frac{x}{4} = \frac{3x}{4} $$
Problema 2 
En cada caso, hallar el número que cumple:
- Su doble más 5 es 35.
- Al sumarle su consecutivo obtenemos 51.
- Al sumarle su doble, su mitad y 15 se obtiene 99.
- Su cuarta parte es 15.
SOLUCIÓN:
El doble de \(x\) es \(2x\), luego obtenemos la ecuación
$$2x + 5 = 35$$
Resolvemos la ecuación:
$$2x = 35-5$$
$$2x = 30$$
$$x = \frac{30}{2}=15$$
Por tanto el número es el 15.
-
Sea \(x\) el número buscado, su consecutivo (el siguiente) se obtiene al sumarle 1. Como la suma de \(x\) y de su consecutivo debe ser 51, tenemos:
$$x + ( x + 1 ) = 51$$
Nota: hemos escrito el paréntesis para distinguir los números, pero no es necesario.
Resolvemos la ecuación:
$$2x +1 = 51$$
$$2x = 50$$
$$x = \frac{50}{2} = 25$$
Por tanto, el número es el 25.
El doble de \(x\) es \(2x\) y la mitad de \(x\) es \(x/2\).
La suma de \(x\), su doble, su mitad y 15 debe ser 99:
$$x + 2x + \frac{x}{2} + 15 = 99$$
Resolvemos la ecuación:
$$3x + \frac{x}{2} = 99-15$$
$$3x + \frac{x}{2} = 84$$
Tenemos que sumar fracciones:
$$\frac{6}{2}x + \frac{1}{2}x = 84$$
$$\frac{7}{2}x = 84$$
$$x = \frac{84\cdot 2}{7}=24$$
Por tanto el número buscado es 24.
La cuarta parte de \(x\) es \(x/4\). Por tanto, tenemos la ecuación
$$\frac{x}{4} = 15$$
$$x=15 \cdot 4 = 60$$
El número es el 60.
Contenido de esta página en versión Kindle:
Problema 3 
Marta tiene 15 años, que es la tercera parte de la edad de su madre. ¿Qué edad tiene la madre de Marta?
SOLUCIÓN:
Llamamos \(x\) a la edad de la madre.
La tercera parte de la edad de la madre es \(x/3\).
Escribimos matemáticamente que la tercera parte de la edad de la madre (\(x/3\)) es la misma que la de Marta (es decir, 15):
$$\frac{x}{3} = 15$$
Resolvemos la ecuación:
$$x = 3\cdot 15$$
$$x = 45$$
Por tanto, la edad de la madre es \(x = 45\).
Problema 4 
¿Cuánto mide una cuerda si su tercera cuarta parte mide 200 metros?
SOLUCIÓN:
Sea \(x\) la longitud de la cuerda.
Sabemos que su tercera cuarta parte es 200, es decir
$$\frac{3x}{4} = 200$$
Resolvemos la ecuación:
$$\frac{3x}{4} = 200$$
$$3x = 4\cdot 200$$
$$x = \frac{4\cdot 200}{3} $$
$$x = 266.667\text{ metros} $$
Por tanto, la cuerda mide aproximadamente 266.667 metros.
Problema 5 
Hallar tres números consecutivos cuya suma sea 219.
SOLUCIÓN:
-
Sea \(x\) el primer número (el menor de ellos).
-
El consecutivo de \(x\) es \(x + 1\).
-
El consecutivo del número \(x+1\) es \(x + 1 + 1\), es decir, \(x+2\).
Como la suma de estos tres números es 219, tenemos la ecuación
$$ x + (x + 1) + (x + 2) = 219$$
Nota: Hemos escrito los paréntesis para que se distingan los 3 números consecutivos, pero no son necesarios.
Resolvemos la ecuación:
$$ x + (x + 1) + (x + 2) = 219$$
$$3x + 3 = 219$$
$$3x = 219-3$$
$$3x = 216$$
$$x = \frac{216}{3} = 72$$
El primer número es \(x = 72\).
Su consecutivo es \(x + 1 = 73\).
El consecutivo del anterior es \(x + 2 = 74\).
Por tanto, los tres números consecutivos que suman 219 son 72, 73 y 74.
Problema 6 
Recorremos un camino de 1 km a una velocidad de 6 km/h. ¿Cuánto tardamos en llegar al destino?
SOLUCIÓN:
Sabemos que el espacio recorrido es igual a la velocidad por el tiempo.
Sea \(x\) el tiempo:
$$\text{Espacio recorrido} = \text{velocidad}\cdot x $$
Sabemos que el espacio recorrido es 1km y la velocidad es 6km/h. Sustituimos en la ecuación:
$$ 1 = 6\cdot x$$
Calculamos \(x\):
$$ x = \frac{1}{6}$$
Tardamos \(x = 1/6 = 0.1667\) horas en llegar.
Nota: el tiempo obtenido es en horas porque el dato de la velocidad del problema es en km/h.
Pasamos de horas a minutos (multiplicando por 60):
$$ 0.1667\cdot 60 = 10.002 \text{ minutos}$$
En realidad, son exactamente 10 minutos, pero obtenemos 10.002 porque hemos aproximado el valor de 1/6.
Nota: no olvidemos comprobar las unidades de medida. Si, por ejemplo, el espacio recorrido
fuese en metros, tendríamos que pasarlo a kilómetros (o cambiar la unidad de la velocidad).
Problema 7 
Héctor guarda 25 euros en su hucha, lo que supone sumar una cuarta parte del dinero que ya había.
-
¿Cuánto dinero hay ahora en la hucha?
-
¿Cuánto dinero debería añadir a la hucha si quiere duplicar el dinero que había inicialmente?
SOLUCIÓN:
Llamamos \(x\) al dinero que había inicialmente en la hucha
Los 25€ que guarda equivalen a la cuarta parte del dinero que había en la hucha, es decir, matemáticamente,
$$ 25 = \frac{x}{4}$$
La solución de la ecuación es
$$ x = 25\cdot 4 = 100$$
Por tanto, en la hucha había 100€ y ahora hay 125€:
$$ 100 + 25 = 125\text{ euros}$$
Para duplicar la cantidad inicial (100€) tiene que haber 200€ en la hucha. Como ahora mismo hay 125€, necesitaría añadir otros 75€:
$$ 200 - 125 = 75 $$
Problema 8 
El padre de Ana tiene 4 años menos que su madre y la mitad de la edad de la madre es 19. ¿Qué edades tienen los padres de Ana? Además, si sabemos que el séxtuple de la edad de Ana es la suma de las edades sus padres, ¿cuál es su edad?
SOLUCIÓN:
Llamamos \(x\) a la edad de la madre de Ana.
-
La mitad de la edad de la madre es 19, por tanto,
$$ \frac{x}{2} = 19$$
Resolviendo la ecuación, la edad de la madre es
$$x = 19\cdot 2 = 38$$
-
Como el padre de Ana tiene 4 años menos que la madre, su edad es 34 años:
$$ 38 - 4 = 34 $$
Luego el padre de Ana tiene 34 años y su madre tiene 38.
Ahora podemos llamar \(x\) a la edad de Ana (sin confundir con la \(x\) anterior). Tenemos:
-
Las edades de sus padres suman 72:
$$ 38 + 34 = 72$$
-
Como 6 veces la edad de Ana es 72,
$$ 6\cdot x = 72 $$
Luego la edad de Ana es
$$ x = \frac{72}{6} = 12 $$
Problema 9 
Carmen tiene 16 años y sus dos hermanos pequeños tienen 2 y 3 años. ¿Cuántos años han de pasar para que el doble de la suma de las edades de los hermanos de Carmen sea la misma que la que tiene ella?
SOLUCIÓN:
Llamamos \(x\) a los años que tienen que pasar para que se cumpla el enunciado del problema.
Cuando pasen estos \(x\) años:
-
El hermano pequeño tendrá \(2+x\) años.
-
El hermano mayor tendrá \(3+x\) años.
-
Carmen tendrá \(16+x\) años.
El doble de la suma de los años de los hermanos ha de ser igual que la de Carmen:
$$2\cdot ( ( 2 + x )+( 3 + x ) ) = 16 + x$$
Obsérvese que el 2 multiplica a la suma de las edades de los hermanos. Es importante escribir dicha suma entre paréntesis.
Resolvemos la ecuación:
$$2\cdot ( ( 2 + x )+( 3 + x ) ) = 16 + x$$
Sumando dentro del paréntesis (sumando las edades de los hermanos), tenemos
$$2\cdot ( 2x + 5) = 16+x$$
Teniendo en cuenta que el 2 multiplica a los dos sumandos de dentro del paréntesis,
$$2\cdot 2x + 2\cdot 5 = 16+x$$
$$4x +10 = 16 + x$$
$$4x-x = 16-10$$
$$3x = 6$$
$$x = \frac{6}{3}=2$$
Es decir, tienen que pasar 2 años.
Problema 10 
Hallar el número tal que si sumamos su mitad con su doble y su triple obtenemos 55.
SOLUCIÓN:
Llamamos \(x\) al número que buscamos. Entonces,
-
\(x/2\) es su mitad
-
\(2x\) es su doble
-
\(3x\) es su triple
Queremos que los 3 números anteriores sumen 55, así que la ecuación resultante es
$$\frac{x}{2} + 2x + 3x = 55$$
Resolvemos la ecuación:
$$\frac{x}{2} + 5x = 55$$
$$\frac{1}{2}\cdot x + \frac{10}{2}\cdot x = 55$$
$$\frac{11}{2}\cdot x = 55$$
$$x = \frac{55 \cdot 2}{11}=10$$
Por tanto, el número buscado es 10.
Problema 11 
Vicente se gasta 20 euros en un pantalón y una camisa.
No sabe el precio de cada prenda, pero sí sabe que la camisa
vale dos quintas partes de lo que vale el pantalón. ¿Cuánto vale
el pantalón?
SOLUCIÓN:
-
Llamamos \(x\) al precio del pantalón.
-
Entonces, el precio de la camisa es $$ \frac{2x}{5}$$
-
Ambos precios suman 20 euros:
$$x + \frac{2}{5}\cdot x = 20$$
Resolvemos la ecuación:
$$\frac{5}{5}\cdot x + \frac{2}{5}\cdot x = 20$$
$$\frac{7}{5}\cdot x = 20$$
$$x = \frac{20 \cdot 5}{7} = \frac{100}{7}=14,2857$$
El pantalón vale 14,29€.
Problema 12 
La diferencia entre dos números es 17. Se pide:
-
Calcular dichos números suponiendo que el doble del menor de ellos es 26.
-
Calcular dichos números suponiendo que 26 es el doble del mayor en lugar del doble del menor.
Nota: son dos problemas distintos para apreciar la importancia de plantear correctamente la ecuación.
SOLUCIÓN:
Primera parte:
Llamamos \(x\) al número menor.
Como la diferencia entre los dos números es 17 y \(x\) es el menor de ellos, entonces el mayor es
$$ x + 17 $$
El doble del menor es 26, así que
$$ 2x = 26$$
Luego
$$ x = \frac{26}{2} = 13$$
Los números buscados son 13 y 30 porque
-
\(x = 13\) es el menor y
-
\(x + 17 = 13 + 17 = 30\) es el mayor.
Segunda parte:
Llamamos \(x\) al número mayor.
Como la diferencia entre los dos es 17, entonces el menor es
$$ x-17$$
El doble del mayor es 26, entonces,
$$ 2x = 26$$
Luego,
$$ x = \frac{26}{2} = 13$$
Los números buscados son 13 y -4 porque
-
\(x = 13\) es el mayor y
-
\(x - 17 = 13 - 17 = -4\) es el menor.
Problema 13 
Hace 5 años la edad de
Ernesto era el triple que la de su primo Juan,
que tiene ahora 15 años. ¿Cuántos años han
de pasar para que Juan tenga la edad actual de Ernesto?
SOLUCIÓN:
Llamamos \(x\) a la edad actual de Ernesto. Entonces,
-
Hace 5 años, Ernesto tenía 5 años menos que ahora, es decir, su edad era $$ x - 5$$
-
Como Juan tiene 15 años, hace 5 años su edad era 10.
-
Para entonces (hace 5 años), la edad de Ernesto (\(x-5\)) era el triple que la de Juan (que tenía 10), así que $$ x - 5 = 3\cdot 10$$
Resolvemos la ecuación:
$$x - 5 = 3\cdot 10$$
$$ x = 30 + 5 $$
Por tanto, \(x = 35\).
Hemos calculado \(x = 35\), que es la edad actual de Ernesto.
Como Juan tiene actualmente 15 años, han de pasar 20 años para que tenga la edad actual de Ernesto, ya que
$$ 15 + 20 = 35 $$
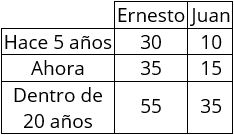
Tabla resumen:
Problema 14 
Tenemos tres peceras y 56 peces. Los tamaños de las peceras
son pequeño, mediano y grande, siendo la pequeña la mitad de la
mediana y la grande el doble. Como no tenemos ninguna preferencia en cuanto al
reparto de los peces, decidimos que en cada una de ellas haya una cantidad de peces
proporcional al tamaño de cada pecera. ¿Cuántos peces pondremos en cada pecera?
SOLUCIÓN:
Sea \(x\) el número de peces en la pecera mediana. Entonces, para que haya proporcionalidad con el tamaño,
-
En la pecera pequeña debe haber \(x/2\) peces, porque es la mitad que la mediana.
-
En la pecera grande debe haber \(2x\) peces, porque es el doble que la mediana.
Ahora bien, como el total de peces es 56, tenemos la ecuación de primer grado
$$x + \frac{x}{2} + 2x = 56$$
Resolvemos:
$$3x + \frac{x}{2} = 56$$
Tenemos que sumar las fracciones:
$$\frac{6x}{2} + \frac{x}{2} = 56$$
$$\frac{7x}{2} = 56$$
La solución es
$$x = \frac{56\cdot 2}{7}= 16$$
Por tanto,
-
Peces en la pequeña: \(16/2=8\).
-
Peces en la mediana: \(16\).
-
Peces en la grande: \(2·16=32\).
Problema 15 
Queremos repartir 510 caramelos entre un grupo de 3
niños, de tal forma que dos de ellos tengan la mitad de los
caramelos pero que uno de estos dos tenga la mitad de caramelos que el otro.
¿Cuántos caramelos tendrá cada niño?
SOLUCIÓN:
La cantidad de caramelos de dos de ellos es la mitad del total, con lo que el otro niño tendrá la otra mitad, es decir, el tercer niño tendrá 510/2 = 255 caramelos.
Ahora quedan los 255 caramelos a repartir entre los dos primeros.
-
Llamamos \(x\) al número de caramelos de uno de los dos primeros niños, el que tiene la mayor cantidad.
-
El otro niño tiene la mitad de \(x\), es decir, \(x/2\).
-
La suma de los caramelos de los dos niños es 255, es decir, tenemos la ecuación
$$ x + \frac{x}{2} = 255$$
Sumamos las fracciones para resolver la ecuación:
$$ x + \frac{x}{2} = 255$$
$$ \frac{2x}{2} + \frac{x}{2} = 255$$
$$ \frac{3x}{2} = 255 $$
$$ x = \frac{255\cdot 2}{3} = 170$$
Por tanto, uno de los niños tiene \(x = 170\) caramelos y el otro tiene \(x /2 = 170/2 = 85\).
La cantidad de caramelos que tiene cada niño es: 255, 170 y 85.
Problema 16 
La tercera parte de las cucharas de la casa estaban en el
lavaplatos y las restantes en el cajón. Pero la mitad
de las cucharas del cajón, que son 15, se llevan a la mesa.
¿Cuántas cucharas hay en el lavaplatos?
SOLUCIÓN:
Llamamos \(x\) al número total de cucharas de la casa. Entonces:
-
En el lavaplatos hay la tercera parte del total, es decir, hay \(x/3\).
-
Las cucharas restantes estaban, inicialmente, en el cajón. Es decir, en el cajón había \(2x/3\) porque la suma de las fracciones \(x/3\) y \(2x/3\) es el total, \(x\):
$$ \frac{2x}{3} + \frac{x}{3} = \frac{3x}{3} = x$$
-
La mitad de las cucharas que había en el cajón es 15. Esto quiere decir que en el cajón había 30, por lo que tenemos la ecuación
$$ \frac{2x}{3} = 30 $$
Resolvemos la ecuación:
$$ \frac{2x}{3} = 30 $$
$$ 2x = 3\cdot 30 $$
$$ 2x = 90 $$
$$ x = \frac{90}{2} = 45$$
Por tanto, en la casa hay un total de 45 cucharas, de las cuales hay:
-
\(x/3 = 45/3 = 15\) en el lavaplatos.
-
15 en el cajón.
-
15 en la mesa.
Problema 17 
Una tienda vende en dos días la tercera
parte de sus productos. Al día siguiente recibe
del almacén la mitad de la cantidad de los productos
vendidos, que son 15 unidades. ¿Cuántas unidades
vendió en los dos primeros días? ¿Cuántas
unidades hay en la tienda después de abastecerla?
SOLUCIÓN:
-
Llamamos \(x\) al número inicial de productos.
-
En los dos primeros días se venden $$\frac{x}{3}$$
-
Al día siguiente se recibe la mitad de la cantidad vendida que es 15, es decir, tenemos la ecuación $$\frac{1}{2}\cdot \frac{x}{3} = 15 $$
Nota: hemos multiplicado por 1/2 la fracción para obtener su mitad. No olvidemos que la multiplicación de fracciones se calcula multiplicando numerador por numerador y denominador por denominador:
$$\frac{1}{2}\cdot \frac{x}{3} = \frac{1\cdot x}{2\cdot 3} = \frac{x}{6}$$
Resolvemos la ecuación que tenemos:
$$ \frac{x}{6} = 15$$
$$ x = 15 \cdot 6 = 90$$
En la tienda había 90 productos.
En los dos primeros días se venden
$$\frac{x}{3} = \frac{90}{3} = 30$$
La cantidad después de la venta y del abastecimiento es: 90 - 30 + 15 = 75 productos.
Problema 18 
Juan tiene 400 euros y Rosa tiene 350. Ambos se compran
el mismo libro. Después de la compra, a Rosa le quedan
cinco sextas partes del dinero que le queda a Juan.
Calcular el precio del libro.
SOLUCIÓN:
Llamamos \(x\) al precio del libro, que obviamente es el mismo para Juan y para Rosa. Entonces,
-
Dinero que le queda a Juan: \(400 - x\)
-
Dinero que le queda a Rosa: \(350 - x\)
El dinero que le queda a Rosa es 5/6 del que le queda a Juan, por tanto,
$$ 350 - x = \frac{5}{6}\cdot ( 400 - x )$$
Pasamos el 6 del denominador multiplicando al otro lado y resolvemos:
$$ 6\cdot (350 - x) = 5 \cdot ( 400 - x )$$
Nota: no olvidemos que el número de delante del paréntesis multiplica a todos los sumandos que contiene.
$$ 6\cdot 350 - 6\cdot x = 5 \cdot ( 400 - x )$$
$$ 2100 - 6x = 5\cdot (400-x) $$
$$ 2100 - 6x = 2000 -5x $$
$$ 2100 - 2000 = 6x -5x$$
$$ 100 = x$$
Por tanto, el precio del libro es \(x = 100\) euros.
Problema 19 
Ester tiene el triple de dinero que Ana y la mitad
que Héctor. Héctor les da a Ana y a
Ester 25 euros a cada una. Ahora Ester tiene
la misma cantidad que Héctor. ¿Cuánto
dinero tenía cada uno al principio? ¿Y después?
SOLUCIÓN:
-
Llamamos \(x\) a la cantidad de dinero que tiene Ana inicialmente.
-
Como Ester tiene inicialmente el triple que el que tiene Ana, Ester tiene inicialmente \(3x\).
-
El dinero inicial de Héctor es el doble que el de Ester, por tanto, es 2 veces \(3x\), es decir, \(2\cdot 3x\), que es lo mismo que \(6x\).
Una vez se realiza el reparto:
-
Héctor tiene 50€ menos, es decir, Héctor tiene \(6x-50\)
-
Ana tiene 25€ más, es decir, Ana tiene \(x + 25\)
-
Ester tiene 25€ más, es decir, Ester tiene \(3x + 25\)
Tras el reparto, sabemos que Ester tiene la misma cantidad que Héctor, con lo que
$$ 3x + 25 = 6x - 50$$
Resolvemos la sencilla ecuación:
$$ 3x + 25 = 6x - 50$$
$$ 50 + 25 = 6x - 3x$$
$$ 75 = 3x$$
$$ x = \frac{75}{3} = 25$$
Calculamos el dinero que tenía y tiene cada uno de ellos sustituyendo \(x = 25\):
Inicialmente tenían:
-
Ester: \(3\cdot 25 = 75\) euros.
-
Ana: \(25\) euros.
-
Héctor: \(6\cdot 25 = 150\) euros.
Después del reparto:
-
Ester: \(75 + 25 = 100\) euros.
-
Ana: \(25 + 25 = 50\) euros.
-
Héctor: \(150 - 50 = 100\) euros.
Problema 20 
En una casa, el depósito de agua se encuentra al 2/7 de su capacidad. Se duchan tres personas: el primero en ducharse consume una quinta parte de la cantidad de agua que hay en el depósito; el segundo, una tercera parte de la cantidad que queda; y el tercero, tres cuartas partes de la cantidad del primero.
¿Cuál es la capacidad del depósito
y la cantidad de agua que consumen los dos
primeros si sabemos que el tercero
consume 10 litros al ducharse?
SOLUCIÓN:
Llamamos \(x\) a la capacidad del depósito (en litros).
Antes de ducharse, el depósito se encuentra al 2/7, es decir, hay
$$\frac{2}{7}\cdot x \text{ litros}$$
El primero consume 1/5 del agua que hay en el depósito, es decir, consume
$$\frac{1}{5} \cdot \frac{2}{7}x = \frac{2}{35}x$$
Como el primero consume 1/5 (un quinto) de \(2x/7\), después de ducharse éste quedan 4/5 (cuatro quintos) de \(2x/7\):
$$\frac{4}{5} \cdot \frac{2}{7}x = \frac{8}{35}x$$
El segundo en ducharse consume la tercera parte de lo que queda, esto es, consume
$$\frac{1}{3} \cdot \frac{8}{35}x = \frac{8}{105}x$$
El tercero consume 3/4 de lo que consume el primero, es decir, consume
$$\frac{3}{4} \cdot \frac{2}{35}x = \frac{6}{140}x =\frac{3}{70}x$$
Sabiendo que el tercero consume 10L, tenemos la siguiente ecuación:
$$\frac{3}{70}x = 10$$
Cuya solución es:
$$x = \frac{700}{3} \simeq 233.33 $$
Una vez calculada \(x\) ya podemos contestar a las preguntas:
-
La capacidad del depósito es de \(x = 700/3 = 233.33\) litros.
-
El primero consume
$$ \frac{2}{35}\cdot \frac{700}{3} = \frac{40}{3} \simeq 13.33 \text{ litros} $$
-
El segundo consume
$$ \frac{8}{105}\cdot\frac{700}{3} = \frac{160}{9} \simeq 17.77 \text{ litros} $$
Problema 21 
¿Cuánto se tarda en recorrer una
distancia de 10km a una velocidad
de 40km/h?
SOLUCIÓN:
Sabemos que el espacio recorrido es la velocidad por el tiempo, es decir,
$$ e = v\cdot t $$
Los datos que tenemos son
-
distancia o espacio recorrido: \( e = 10 \text{ km}\).
-
velocidad: \( v = 40 \text{ km/h}\).
Nota: obsérvese que las unidades del espacio coinciden en ambos datos (km y km/h). Al aplicar la fórmula, el tiempo será en horas (porque la velocidad es en km/h).
Como tenemos las mismas unidades (en kilómetros), sólo
tenemos que sustituir en la ecuación y despejar la
\(t\), que estará dada en horas.
Sustituimos en la ecuación \( e = v \cdot t\):
$$ 10 = 40\cdot t$$
Resolvemos la ecuación:
$$ t= \frac{10}{40} =\frac{1}{4} = 0.25\text{ h}$$
Podemos pasar el tiempo a minutos multiplicándolo por 60:
$$ t = 0.25\cdot 60 = 15 \text{ min}$$
Consejo: podemos escribir las unidades en la propia ecuación y tratarlas como factores de la misma. Así, cuando tenemos una gran cantidad y variedad de unidades, es más fácil saber cuál es la unidad del resultado. En este problema tendríamos:
$$10\text{ km} = \frac{40\text{ km}}{\text{h}}\cdot t $$
Despejamos la \(t\):
$$ t = \frac{10\text{ km}}{40\text{ km}} \text{ h}$$
Y ahora, como \(km\) está "multiplicando" en el numerador y en el denominador, los podemos eliminar:
$$ t = \frac{10}{40}\text{ h} = \frac{1}{4}\text{ h} = 0.25\text{ h} = 15\text{ min}$$
Problema 22 
¿Cuántos minutos se tarda en recorrer
una distancia de 108km a
una velocidad de 120m/h?
SOLUCIÓN:
De nuevo, el espacio o la distancia recorrida es la velocidad por el tiempo, es decir,
$$ e = v\cdot t $$
Como queremos saber el tiempo, \(t\), vamos a despejar la \(t\) antes de sustituir los
datos en la fórmula:
$$ e = v\cdot t \ \rightarrow \ t =\frac{e}{v} $$
Tenemos los datos
-
Distancia: \(e = 108 \text{ km}\)
-
Velocidad: \( v = 120 \text{ m/h}\)
Tenemos las unidades de distancia en kilómetros (en la \(e\)) y en metros (en la \(v\)), así que tenemos que pasarlas a la misma unidad. Escribiremos la velocidad en km/min para que coincidan. De este modo tenemos km en ambos datos y, además, obtendremos el tiempo en minutos.
$$ v = \frac{120m}{h} = \frac{120:1000km}{1\cdot 60min} $$
Nota: hemos dividido por 1000 para pasar de metros a kilómetros y multiplicado por 60 para pasar de horas a minutos. Haciendo los cálculos:
$$ v = \frac{0.12 km}{60min} = 0.002 km/min$$
Ahora, sustituimos los datos y obtenemos el tiempo
$$ t = \frac{e}{v} = \frac{108km}{0.002km/min} = \frac{108}{0.002} \ min = 54000\ min $$
Nota: como min está "dividiendo" en el denominador, pasa "multiplicando" en el numerador; km desaparece porque está "multiplicando" en el numerador y en el denominador.
Nota 2: el resultado del problema obtenido es muy alto porque 120m/h es una velocidad muy lenta. Por ejemplo, las personas caminamos a unos 5.000m/h (ó 5km/h), lo cual es más de 41 veces más rápido que la velocidad de este problema.
Problema 23 
¿Cuántos kilómetros se recorren si se circula a
una velocidad constante
de 5m/s durante dos horas?
SOLUCIÓN:
Usaremos la misma fórmula:
$$ e = v\cdot t $$
Conocemos los datos
-
Velocidad: \( v = 5\text{ m/s}\)
-
Tiempo: \( t = 2\text{ h}\)
Tenemos distintas unidades de tiempo (horas y segundos), así que pasamos el tiempo a segundos:
$$ t=2\text{ h} = 2\cdot 60\text{ min} =$$ $$ = 120\text{ min} = 120\cdot 60\text{ s} =7200\text{ s} $$
No pasamos todavía los 5m a km para no trabajar con decimales.
Finalmente, sustituimos en la ecuación y pasamos el resultado a kilómetros:
$$ e = v\cdot t $$ $$e = \frac{5\text{ m}}{\text{s}} \cdot 7200\text{ s} = 36000\text{ m} =36\text{ km}$$
Por tanto, se recorren 36km si se circula a una velocidad de 5m/s durante 2h.
Problema 24 
En un maratón de 45 km, el ganador corrió a una velocidad media de
16 km/h mientras que el último clasificado lo hizo a 7.5 km/h.
¿Cuánto tiempo tardaron en llegar a la meta cada uno de ellos?
SOLUCIÓN:
Usaremos la forma que venimos usando en los problemas anteriores:
$$ e = v\cdot t $$
Como queremos saber el tiempo, \(t\), vamos a despejar la \(t\) antes de sustituir los
datos en la ecuación:
$$ e = v\cdot t \ \rightarrow \ t =\frac{e}{v} $$
Sustituimos los datos para el ganador:
$$ t= \frac{45\text{ km}}{16\text{ km/h}} = 2.81\text{ h} \simeq 2\text{ h}\ 48\text{ min} $$
Para escribir el tiempo en horas y en minutos hemos realizado las siguientes operaciones:
$$2.81\text{ h} = 2\text{ h} +0.81\text{ h} =$$ $$= 2\text{ h} + 0.81\cdot 60\text{ min} \simeq 2\text{ h}\ 48\text{ min}$$
Sustituimos los datos para el último clasificado:
$$ t= \frac{45\text{ km}}{7.5\text{ km/h}} = 6\text{ h}$$
Por tanto, el primer clasificado tardó unas 2h y 48min y el último tardó 6h.
Problema 25 
La distancia entre las ciudades A y B es de 50 km. A la misma hora, salen un camión de la ciudad A a 60 km/h y un ciclista de la ciudad B a 25 km/h. Se desea calcular cuánto tardarán en encontrarse si ambos vehículos circulan por la misma carretera pero en sentido opuesto.
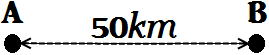
SOLUCIÓN:
Tenemos los siguientes datos iniciales:
-
Ecuación del espacio recorrido en función de la velocidad y del tiempo:
$$e=v\cdot t$$
-
Velocidad del camión:
$$ v_c = 60km/h$$
-
Velocidad de la bicicleta:
$$ v_b = 25km/h$$
Cuando los dos vehículos se encuentran, el camión ha recorrido una distancia mayor que el ciclista (ya que su velocidad es mayor). Como no conocemos esta distancia, la llamaremos \(x\). Asimismo, el ciclista habrá recorrido \(50-x \text{ km}\).
El esquema del problema es el siguiente:
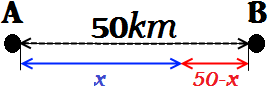
A los datos iniciales tenemos que añadir el espacio recorrido por el camión
$$ e_c=x $$
y el recorrido por la bicicleta
$$ e_b = 50-x$$
Los tiempos son los mismos ya que ambos salen en el mismo instante:
$$ t_c = t_b $$
Sustituimos en la ecuación los datos del camión:
$$ e_c=v_c \cdot t_c $$
$$ x=60\cdot t_c $$
$$ t_c = \frac{x}{60}$$
Por otro lado, si sustituimos los datos de la bicicleta tenemos
$$ e_b=v_b \cdot t_b $$
$$ 50-x=25\cdot t_b $$
$$ t_b = \frac{50-x}{25}$$
Pero, como ya hemos dicho anteriormente, los tiempos son el mismo para
ambos vehículos y, por tanto, podemos igualarlos obteniendo así una ecuación de primer
grado:
$$ t_c = t_b $$
$$ \frac{x}{60} = \frac{50-x}{25} $$
Resolvemos la ecuación:
$$ 25x = 3000 - 60x$$
$$ 85x = 3000$$
$$ x = \frac{3000}{85} \simeq 35.3$$
Por tanto, cuando se encuentran, el camión ha recorrido unos 35.3 km y el ciclista 50 - 35.3 = 14.7 km.
Como queremos saber el tiempo, sustituimos en cualquiera de las dos ecuaciones que tenemos:
$$ t_c = \frac{x}{60} =$$ $$ = \frac{35.3\text{ km}}{60\text{ km/h}} \simeq 0.59\text{ h} = 35.4\text{ min}$$
Problema para pensar
Encontrar el mayor y el menor número positivo de tres cifras en los que la segunda cifra es el triple de la primera y la tercera el cuádruple de la primera.