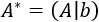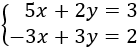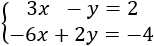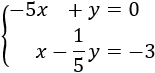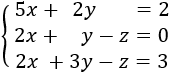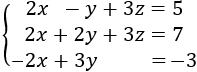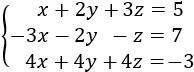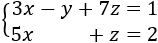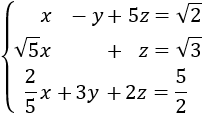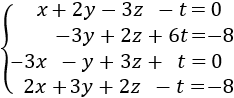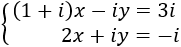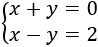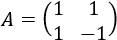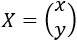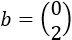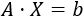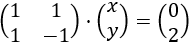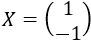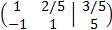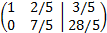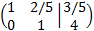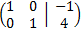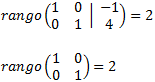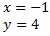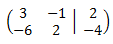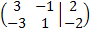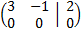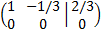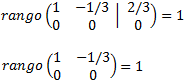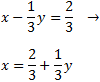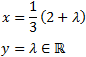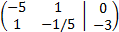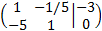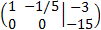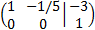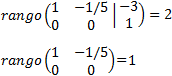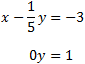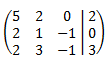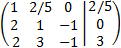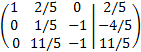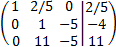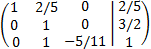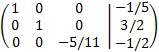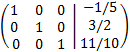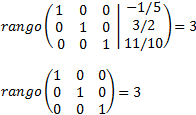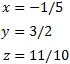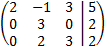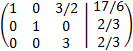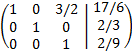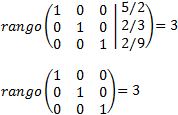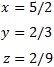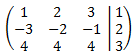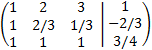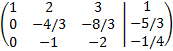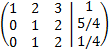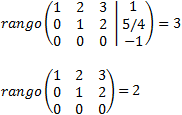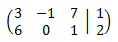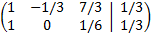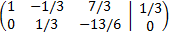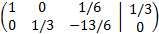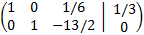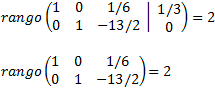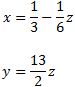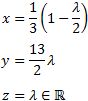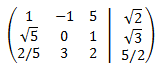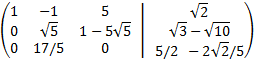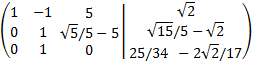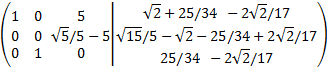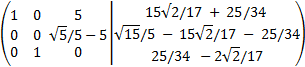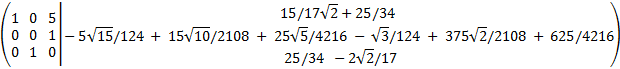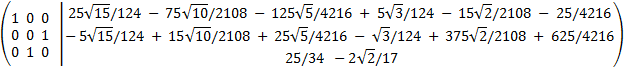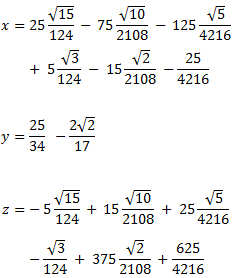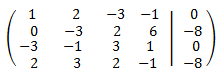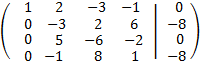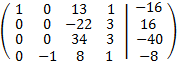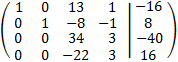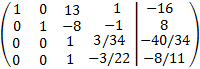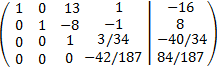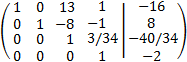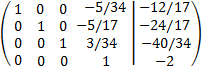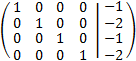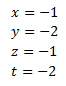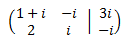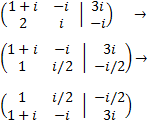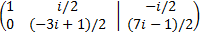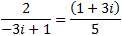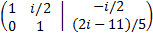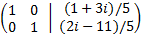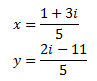Comentario: el método más rápido para resolver un SEL es estudiar el rango de la matriz para determinar el tipo de sistema. Si es SCD, aplicamos la regla de Cramer. Si es SCI, eliminación de Gauss. Si es SI, no hay que realizar cálculos.
Sistema 1 (dimensión 2x2)
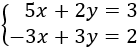
Ver solución
La matriz ampliada del sistema es

La raya vertical separa la matriz de coeficientes de la matriz columna de términos independientes.
Realizamos operaciones elementales fila para obtener la matriz en forma escalonada reducida:
Multiplicamos la primera fila por 1/5 y la segunda por 1/3:
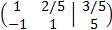
Sumamos a la segunda fila la primera:
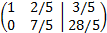
Multiplicamos la segunda fila por 5/7:
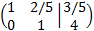
Sumamos a la primera fila la segunda fila multiplicada por -2/5:
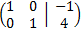
Esta última matriz equivalente ya tiene forma escalonada reducida y nos permite ver rápidamente los rangos
de la matriz de coeficientes y de la ampliada.
Calculamos los rangos de la matriz coeficientes y de la matriz ampliada
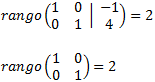
Como los rangos son iguales y máximos, por el Teorema de Rouché-Frobenius, el sistema es compatible determinado. La matriz obtenida representa el sistema
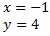
Es la solución del sistema.
Sistema 2 (dimensión 2x2)
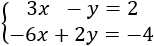
Ver solución
La matriz ampliada del sistema es
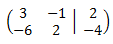
Multiplicamos la segunda fila por 1/2:
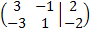
Sumamos la primera fila a la segunda:
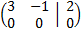
Multiplicamos la primera fila por 1/3:
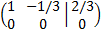
Esta última matriz tiene forma escalonada reducida y tiene una fila nula, lo que significa que
las ecuaciones del sistema son linealmente dependientes. Luego tenemos un sistema con 2 incógnitas y 1 ecuación y, por tanto, indeterminado.
Calculamos los rangos
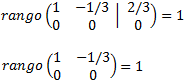
Como los rangos son iguales, por el Teorema de Rouché-Frobenius, el sistema es compatible. Además, es indeterminado, ya que el rango es menor que el número de incógnitas (1 < 2).
La matriz obtenida representa el sistema con una única ecuación
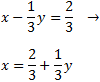
Las soluciones del sistema son
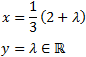
Sistema 3 (dimensión 2x2)
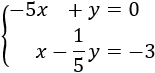
Ver solución
La matriz ampliada del sistema es
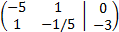
Cambiamos el orden de las filas (de este modo ya tendremos un 1 principal en la primera fila sin necesidad
de multiplicar):
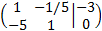
Le sumamos a la segunda fila la primera multiplicada por 5:
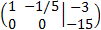
Multiplicamos la segunda fila por -1/15:
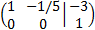
Esta última matriz es la matriz escalonada (no reducida porque todavía podríamos hacer 0 uno de los términos
independientes). Podemos observar directamente que el sistema es incompatible ya que
tenemos la siguiente ecuación (segunda fila):
$$0x + 0y = 1$$
Calculamos los rangos de las matrices ampliada y de coeficientes:
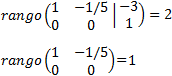
Como los rangos son distintos, por el Teorema de Rouché-Frobenius, el sistema es incompatible (no tiene solución).
La matriz obtenida representa el sistema
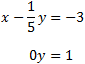
Sistema 4 (dimensión 3x3)
Ver solución
La matriz ampliada del sistema es
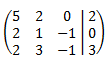
Es una matriz de dimensión 3x4.
Multiplicamos la primera fila por 1/5:
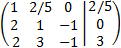
Sumamos a la segunda y tercera fila la primera multiplicada por -2:
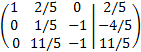
Multiplicamos las filas segunda y tercera por 5:
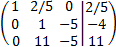
Sumamos a la segunda fila la tercera multiplicada por -1:

Multiplicamos la segunda fila por -1/10 y la tercera por 1/11:
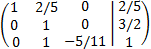
Sumamos a la primera fila la segunda multiplicada por -2/5 y a la tercera, la segunda por -1:
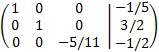
Multiplicamos la tercera fila por -11/5:
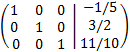
Esta última matriz tiene forma escalonada reducida (es la matriz identidad).
Realmente, ya tenemos la solución del sistema, así que es un sistema compatible determinado.
No obstante, calculamos los rangos:
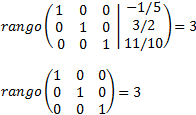
Como los rango son iguales y máximos, por el Teorema de Rouché-Frobenius, el sistema es compatible determinado. La matriz obtenida proporciona la solución del sistema:
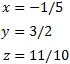
Sistema 5 (dimensión 3x3)
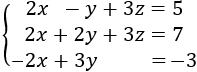
Ver solución
La matriz ampliada del sistema es

Realizamos operaciones elementales fila para obtener la matriz en forma escalonada reducida:
A la segunda fila le restamos la primera y a la tercera se la sumamos:
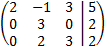
Multiplicamos la primera fila por 1/2 y la segunda por 1/3:

Sumamos a la primera fila la segunda multiplicada por 1/2 y a la tercera, la segunda multiplicada por -2:
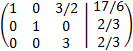
Multiplicamos la tercera fila por 1/3:
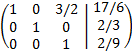
Sumamos a la primera fila la tercera multiplicada por -3/2:

Esta última matriz es la escalonada reducida (lo sabemos porque tenemos la matriz identidad).
Calculamos los rangos:
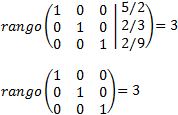
Como los rangos coinciden y son máximos, por el Teorema de Rouché-Frobenius, el sistema es compatible determinado. La solución del sistema es
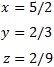
Sistema 6 (dimensión 3x3)
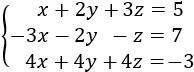
Ver solución
La matriz ampliada del sistema es
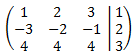
Multiplicamos la segunda fila por -1/3 y la tercera por 1/4:
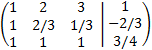
Sumamos a las filas segunda y tercera la primera multiplicada por -1:
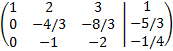
Multiplicamos la segunda fila por -3/4 y la tercera por -1:
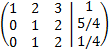
Sumamos a la tercera fila la segunda multiplicada por -1:

Esta última matriz tiene forma escalonada (pero no reducida) y no continuamos realizando operaciones
fila ya que vemos que la última fila hace que el sistema sea incompatible. Dicha fila representa la ecuación
$$0x+0y+0z = -1$$
En efecto, los rangos de la ampliada y la matriz de coeficientes son
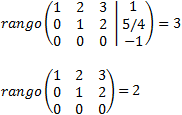
Como son distintos, por el Teorema de Rouché-Frobenius, el sistema es incompatible.
Sistema 7 (dimensión 2x3)
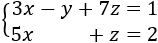
Ver solución
La matriz ampliada del sistema es
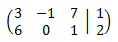
Realizamos operaciones elementales fila para obtener la matriz en forma escalonada reducida
Multiplicamos las filas primera y segunda por 1/3 y por 1/6, respectivamente:
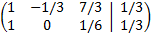
Restamos a la segunda fila la tercera:
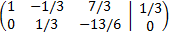
Sumamos a la primera fila la segunda:
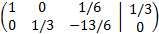
Multiplicamos la tercera fila por 3:
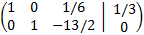
Esta última matriz ya tiene forma escalonada reducida, por lo que podemos calcular fácilmente los rangos:
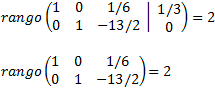
Como son iguales, por el Teorema de Rouché-Frobenius, el sistema es compatible indeterminado. Es indeterminado porque el número de incógnitas es mayor que el de ecuaciones.
La matriz obtenida representa el sistema
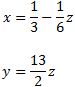
Las soluciones del sistema son
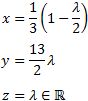
Sistema 8 (dimensión 3x3)
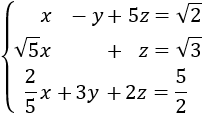
Ver solución
La matriz ampliada del sistema es
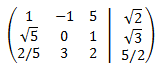
Nota: antes de empezar, comentamos que la presencia de raíces en la matriz va a complicar un poco las operaciones.
Sumamos a la segunda fila la primera multiplicada por \(-\sqrt{5}\) y, a la tercera, multiplicada por -2/5:
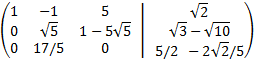
Multiplicamos la segunda fila por \(1/\sqrt{5}\) y la tercera por 5/17:
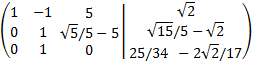
Sumamos a la primera fila la tercera y a la segunda le restamos la tercera:
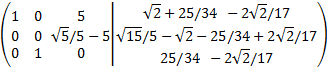
Reescribimos la matriz:
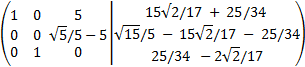
Multiplicamos la segunda fila por \(1/(\sqrt{5}/5 -5)\):
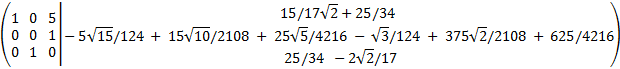
Sumamos a la primera fila la segunda multiplicada por -5:
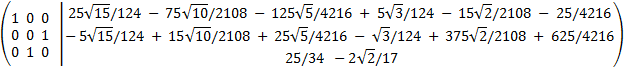
Esta última matriz es casi la forma escalonada reducida. Tenemos que cambiar las segunda y tercera para que
realmente lo sea.
Como los rangos de las matrices amplicada y de coeficientes son ambos 3, por el Teorema de Rouché-Frobenius, el sistema es compatible determinado. De la última matriz obtenemos la solución:
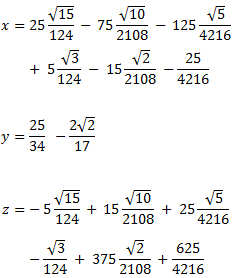
Sistema 9 (dimensión 4x4)
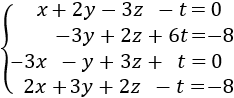
Ver solución
La matriz ampliada del sistema es
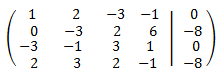
Realizamos operaciones elementales fila para obtener la matriz en forma escalonada reducida:
Sumamos a las filas tercera y cuarta la primera multiplicada por 3 y por -2, respectivamente:
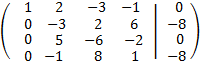
Sumamos a las filas primera, segunda y tercera la cuarta multiplicada por 2, -3 y 5, respectivamente:
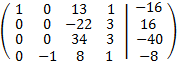
Multiplicamos la cuarta fila por -1 y la intercambiamos con la segunda:
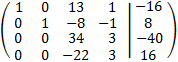
Multiplicamos las filas tercera y cuarta por 1/34 y -1/22, respectivamente:
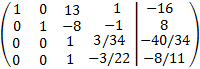
Le restamos la tercera fila a la cuarta:
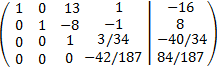
Multiplicamos la cuarta fila por -187/42:
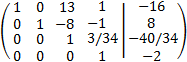
Le sumamos a las filas primera y segunda la tercera multiplicada por -13 y 8, respectivamente:
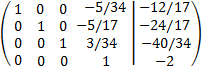
Le sumamos a las filas primera, segunda y tercera la cuarta multiplicada por 5/34, 5/17 y -3/34, respectivamente:
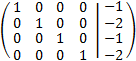
Por el Teorema de Rouché-Frobenius, el sistema es compatible determinado y su solución es
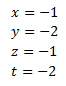
Sistema 10 (dimensión 2x2)
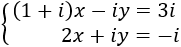
Ver solución
La matriz ampliada del sistema es
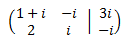
Nota: este sistema se ha incluido con la finalidad de hacer notar que la teoría de matrices
es aplicable al cuerpo de los complejos. La única diferencia con los sistemas
anteriores es que ahora tendremos que efectuar el producto y el cociente de número complejos.
Multiplicamos la segunda fila por 1/2 y la intercambiamos con la primera:
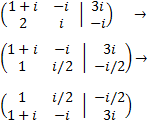
Sumamos a la segunda fila la primera multiplicada por –(1+i):
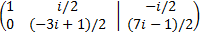
Multiplicamos la segunda fila por
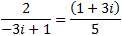
Obtniendo la matriz
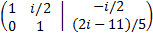
Sumamos a la primera fila la segunda multiplicada por -i/2:
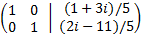
Por el Teorema de Rouché-Frobenius, el sistema es compatible determinado y su solución es
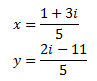


Eliminación de Gauss y de Gauss-Jordan -
© -
matesfacil.com

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.