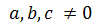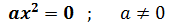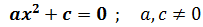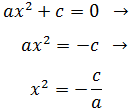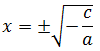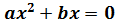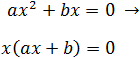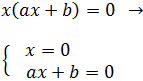Ecuaciones de Segundo Grado Incompletas
Contenido de esta página:
Breve Introducción
-
Ecuaciones Incompletas
-
Obtención de las Soluciones (según los tipos)
-
10 Ecuaciones Resueltas
Introducción
En esta sección vamos a resolver ecuaciones de segundo grado incompletas de los tres tipos. Recordemos que una ecuación de segundo grado, completa o no, puede tener, a lo sumo, dos raíces (reales) distintas.
Aquí podemos acceder a la sección de ecuaciones de segundo grado completas.
1. Ecuación Incompleta
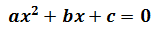
2. Obtención de las Soluciones (según los tipos)
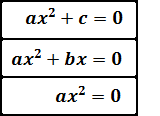
Resolución de Ecuaciones de Segundo Grado Incompletas
Nota: en la resolución de las ecuaciones mostramos la gráfica de la parábola que representa la ecuación. Es decir, la función
$$ f(x) = ax^2 +bx+c $$
Como las soluciones de la ecuación son los puntos donde \(f\) es 0, los puntos de corte de la parábola con el eje de abscisas están en los puntos cuya primera coordenada es la solución de la ecuación y la segunda coordenada es 0. Además, si \(a >0\), entonces la parábola tiene forma de U; si no, tiene forma de U invertida.
Ecuación 1
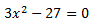
Despejamos x y hacemos la raíz cuadrada (no olvidemos el doble signo)
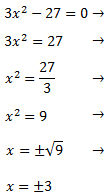
La ecuación tiene dos raíces y la podemos escribir en forma factorizada como
$$3(x+3)(x-3)=0$$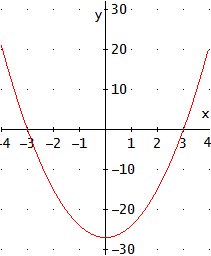
Ecuación 2
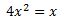
Factorizamos la expresión y nos queda un producto de x por una ecuación.
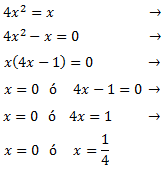
La ecuación tiene dos raíces y la podemos escribir en forma factorizada como
$$4x(x-\frac{1}{4})=0$$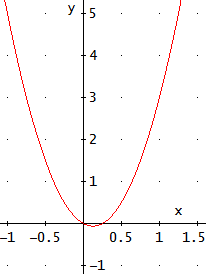
Ecuación 3
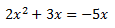
Factorizamos la expresión y nos queda un producto de x por una polinomio de primer grado. Por tanto, el producto es 0 si uno de los dos factores es 0:
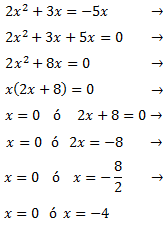
La ecuación tiene dos raíces y la podemos escribir en forma factorizada como
$$2x(x+4)=0$$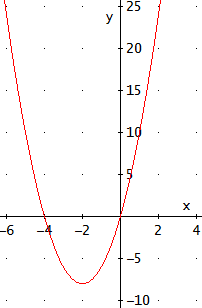
Ecuación 4
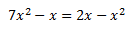
Agrupamos los monomios según su parte literal. Factorizamos la expresión y nos queda un producto de x por un polinomio de primer grado. Por tanto, el producto es 0 si x = 0 o el polinomio es 0:
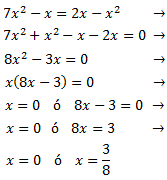
La ecuación tiene dos raíces y la podemos escribir en forma factorizada como
$$8x(x-\frac{3}{8})=0$$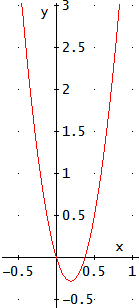
Ecuación 5
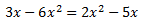
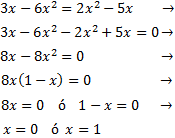
La ecuación tiene dos raíces y la podemos escribir en forma factorizada como
$$-8x(x-1)=0$$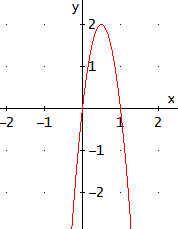
Ecuación 6
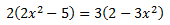
Desarrollamos los paréntesis y despejamos x hacemos la raíz cuadrada:
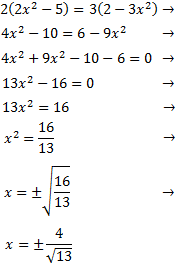
La ecuación tiene dos raíces y la podemos escribir en forma factorizada como
$$13(x-\frac{4}{\sqrt{13}})(x+\frac{4}{\sqrt{13}})=0$$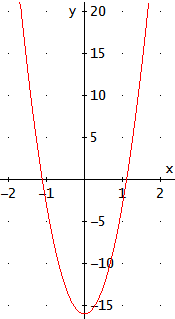
Ecuación 7
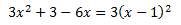
En esta ecuación tenemos un binomio de Newton: ( x - 1 ) 2 = x 2 +1 -2x
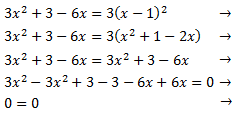
Si obtenemos una igualdad evidente, como 0 = 0, quiere decir que la ecuación se cumple independientemente del valor de x.
La ecuación tiene infinitas soluciones:
$$ x\in \mathbb{R}$$
No representamos esta función puesto que la ecuación es equivalente a 0, es decir, \( a = b = c = 0\).
Ecuación 8
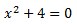
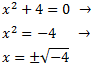
No tiene solución (real) ya que las raíces de los negativos no son números reales (son imaginarios o complejos).
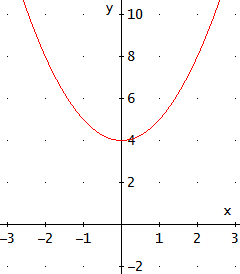
Ecuación 9
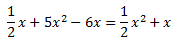
Como tenemos fracciones, vamos a multiplicar toda la ecuación por 2 para evitarlas:
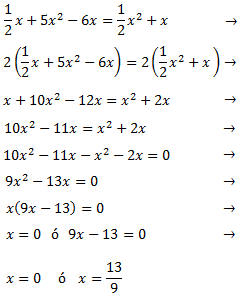
La ecuación tiene dos raíces y la podemos escribir en forma factorizada como
$$\frac{9}{2}x(x-\frac{13}{9})=0$$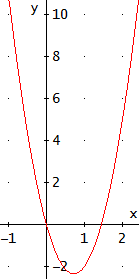
Ecuación 10
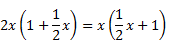
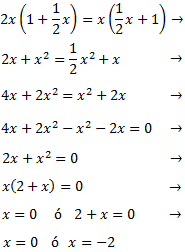
La ecuación tiene dos raíces y la podemos escribir en forma factorizada como
$$\frac{1}{2}x(x+2)=0$$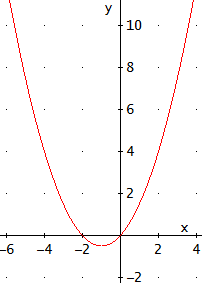
Páginas Relacionadas:

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.