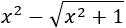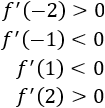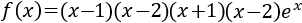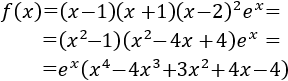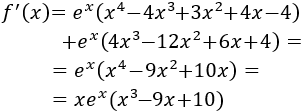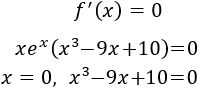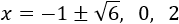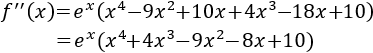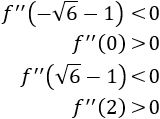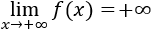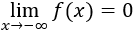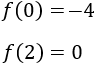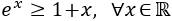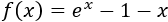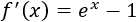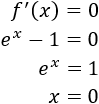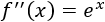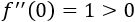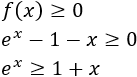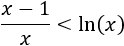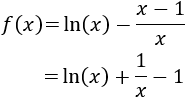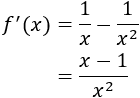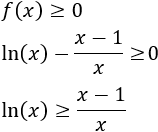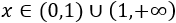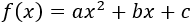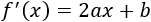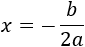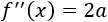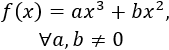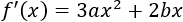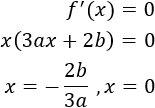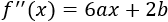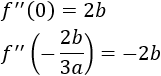Nota 1: aunque podemos deducir la monotonía a partir de los extremos, aplicaremos el criterio de la segunda derivada para ello.
Nota 2: recordad que la derivada de una función \(f\) es un límite:
$$ f'(x) := \lim_{h\to 0} \frac{f(x+h)-f(x)}{h} $$
Por tanto, para que exista la derivada, deben existir y coincidir los límites cuando \(h\) tiende 0 por ambos lados.
En las funciones definidas a trozos, puede darse el caso de que los límites no coincidan en los puntos donde \(x\) cambia de definición. Por esta razón, escribiremos a veces signos estrictos en la primera y segunda derivada.
Función 1
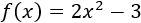
Solución
Dominio:
Como es una función polinómica, el dominio es el conjunto de los reales, \(\mathbb{R}\).
Extremos:
Calculamos la derivada:
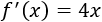
Calculamos los puntos críticos:
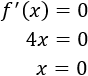
El único punto crítico es \(x = 0\).
Calculamos la segunda derivada:
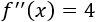
Evaluamos la segunda derivada en el punto crítico:
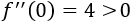
Como la segunda derivada es positiva, se trata de un mínimo.
Observad que la función es un polinomio de grado 2, así que se trata de una parábola. Por tanto, el mínimo es el vértice, por lo que es un mínimo absoluto.
Monotonía:
Estudiamos el signo de la derivada en los intervalos construidos a partir del punto crítico:
![signos negativo en ]-∞0[ y signo positivo en ]0,+∞[ Recordamos los conceptos de extremos relativos y absolutos (máximos y mínimo) y los criterios de la primera y la segunda derivada. Resolvemos 20 problemas de aplicación. Extremos de funciones. Matemáticas. Cálculo diferencial.](https://www.matesfacil.com/BAC/extremos/F1-5.png)
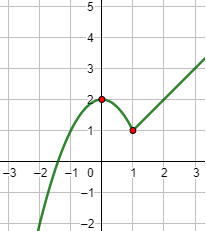
La función es decreciente en \(]-\infty ,0[\) y creciente en \(]0,+\infty [\).
Gráfica:
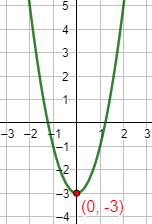
Función 2
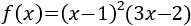
Solución
Dominio:
Como la función es polinómica, el dominio es el conjunto de los reales.
Extremos:
Vamos a desarrollar los productos porque así es más fácil calcular la derivada:
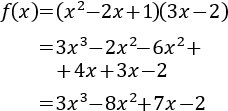
Calculamos la derivada:
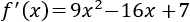
Calculamos los puntos críticos:
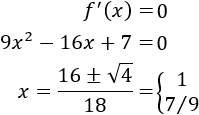
Hay dos puntos críticos: \(x=1\) y \(x=7/9\).
Calculamos la segunda derivada:
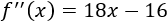
Evaluamos la segunda derivada en los puntos críticos:
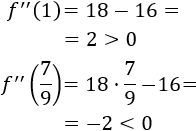
La función tiene un mínimo en \(x=1\) y un máximo en \(x=7/9\).
Los extremos son relativos porque la función no está acotada inferior ni superiormente:
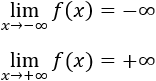
Monotonía:
A la izquierda del mínimo y a la derecha del máximo la función es decreciente (derivada primera negativa).
A la derecha del mínimo y a la izquierda del máximo la función es creciente (derivada primera positiva).
Gráfica:
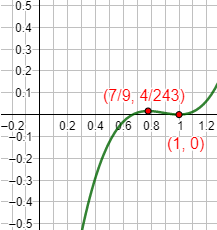
Función 3
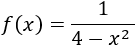
Solución
Dominio:
Como la función es racional, hay que excluir del dominio a los puntos que anulan el denominador.
Igualamos a 0 el denominador y resolvemos la ecuación:
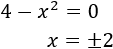
Por tanto, el dominio es
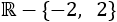
Extremos:
Calculamos la derivada:
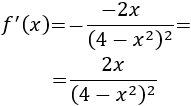
Calculamos los puntos críticos:
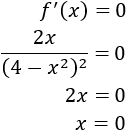
Sólo hay un punto crítico: \(x =0\).
Calculamos la segunda derivada:
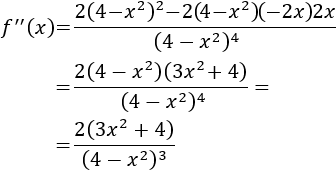
Evaluamos la segunda derivada en el punto crítico:
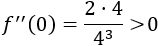
Se trata de un mínimo.
No es un mínimo absoluto porque la función no es acotada inferiormente:
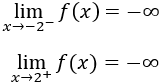
Monotonía:
Tenemos que estudiar el signo de la primera derivada en los intervalos que conforman el dominio junto con los que genera el extremo:
![]-∞,-2[ U ]-2,0[ U ]0,2[ U ]2,+∞[ Recordamos los conceptos de extremos relativos y absolutos (máximos y mínimo) y los criterios de la primera y la segunda derivada. Resolvemos 20 problemas de aplicación. Extremos de funciones. Matemáticas. Cálculo diferencial.](https://www.matesfacil.com/BAC/extremos/F3-8.png)
Elegimos un punto al azar en cada intervalo y evaluamos la derivada (observad que el signo de \(f'(x)\) coincide con el de \(x\) porque el denominador siempre es positivo):
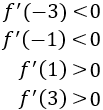
Por tanto, la función es decreciente en \( (-\infty , -2) \cup (-2,0)\) y creciente en \((0,2)\cup (2,+\infty)\).
Gráfica:
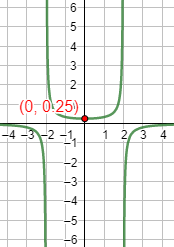
Función 4
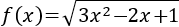
Solución
Dominio:
Como el radicando debe ser no negativo, tiene que cumplirse la inecuación
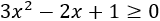
La ecuación \(0 = 3x^2 -2x+1\) no tiene raíces, así que es de signo constante, y como \(3·0^3-2·0+1\) es positivo, la inecuación siempre se cumple.
Por tanto, el dominio de \(f\) es el conjunto de los reales.
Extremos:
Calculamos la derivada:
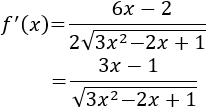
Calculamos los puntos críticos:
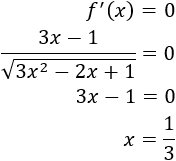
Sólo hay un punto crítico: \(x = 1/3\).
Calculamos la segunda derivada:
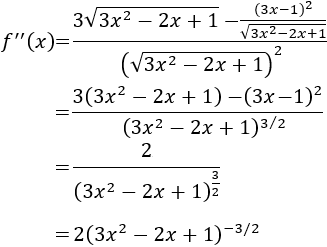
Evaluamos la segunda derivada en el punto crítico:
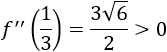
Se trata de un mínimo.
Es un mínimo absoluto (por ser una función irracional).
Observad que sería más rápido deducir que \(x=1/3\) es un mínimo a partir de la monotonía que tener que calcular y evaluar la segunda derivada.
Monotonía:
Lógicamente, la función decrece a la izquierda del mínimo y crece a su derecha, pero vamos a estudiar el signo de la derivada:
![la derivada es negativa en el intervalo ]-∞,1/3[ y es positiva en ]1/3,+∞[ Recordamos los conceptos de extremos relativos y absolutos (máximos y mínimo) y los criterios de la primera y la segunda derivada. Resolvemos 20 problemas de aplicación. Extremos de funciones. Matemáticas. Cálculo diferencial.](https://www.matesfacil.com/BAC/extremos/F4-6.png)
La función decrece en \((-\infty , 1/3)\) y crece en \((1/3,+\infty)\).
Gráfica:
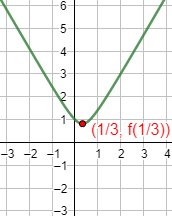
Función 5
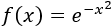
Solución
Dominio:
El dominio es el conjunto de los reales.
Extremos:
Calculamos la derivada:
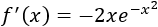
Calculamos los puntos críticos:
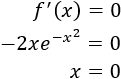
El único punto crítico es \(x=0\).
Calculamos la segunda derivada:
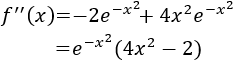
Evaluamos la segunda derivada en \(x=0\):
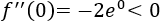
Por tanto, se trara de un máximo.
Monotonía:
Estudiamos el signo de la derivada:
![la derivada es positiva en el intervalo ]-∞,0[ y negativa en ]0,+∞[ Recordamos los conceptos de extremos relativos y absolutos (máximos y mínimo) y los criterios de la primera y la segunda derivada. Resolvemos 20 problemas de aplicación. Extremos de funciones. Matemáticas. Cálculo diferencial.](https://www.matesfacil.com/BAC/extremos/F5-5.png)
Por tanto, \(f\) es creciente el los reales negativos y decreciente en los positivos.
El máximo es un extremo absoluto.
Gráfica:
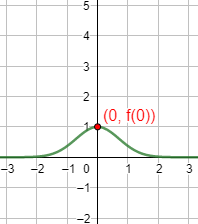
Función 6
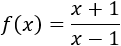
Solución
Dominio:
El dominio de la función es
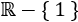
Extremos:
Calculamos la derivada:
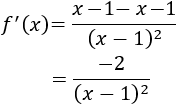
No hay puntos críticos puesto que la derivada nunca se anula:
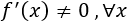
Por tanto, no la función no tiene extremos.
Monotonía:
Como la primera derivada es negativa, la función es decreciente en todo su dominio.
Gráfica:
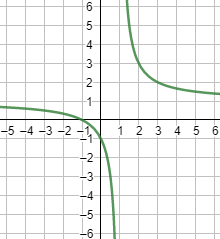
Función 7
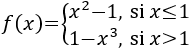
Solución
Dominio:
El dominio es \(\mathbb{R}\).
Extremos:
Calculamos la derivada, que es una función definida a trozos:
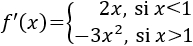
Calculamos los puntos críticos, igualando a 0 ambas definiciones de la derivada:
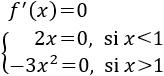
Sólo hay un punto crítico: \(x=0\). Sin embargo, tenemos que considerar al punto \(x=1\) como posible extremo ya que es donde cambia la definición.
Calculamos la segunda derivada:
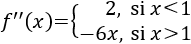
Evaluamos la segunda derivada en \(x=0\):
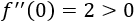
Se trata de un mínimo, pero no es absoluto porque la función decrece infinitamente para \(x> 1\).
Para saber si hay extremo en \(x=1\), tenemos que estudiar la monotonía de la función en el entorno del punto.
Monotonía:
Estudiamos el signo de la primera derivada:
![derivada negativa en ]-∞,0[, positiva en ]0,1[ y negativa en ]1,+∞[ Recordamos los conceptos de extremos relativos y absolutos (máximos y mínimo) y los criterios de la primera y la segunda derivada. Resolvemos 20 problemas de aplicación. Extremos de funciones. Matemáticas. Cálculo diferencial.](https://www.matesfacil.com/BAC/extremos/F7-5.png)
La función decrece en \(x< 0\) y en \(x> 1\) y crece en \((0,1)\). Por tanto, en \(x=1\) hay un máximo. Este extremo no es absoluto porque la función tiende a infinito cuando \(x\to -\infty\):
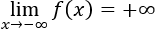
Gráfica:
Función 8
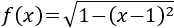
Solución
Dominio:
El radicando debe ser positivo:
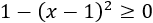
Resolvemos la inecuación:
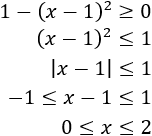
El dominio es \([0,2]\).
Extremos:
Calculamos la derivada:
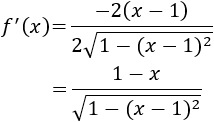
Calculamos los puntos críticos:
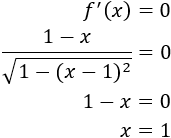
Sólo hay un punto crítico: \(x = 1\). Sin embargo, como el dominio de la función es un intervalo acotado (y cerrado), tenemos que ver también si tiene un extremo en \(x=0\) ó \(x=2\).
Calculamos la segunda derivada:
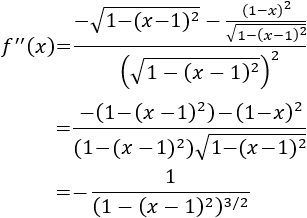
Evaluamos la segunda derivada en \(x=1\):
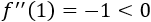
Se trata de un máximo y es absoluto porque la función está acotada.
Como consecuencia, la función crece a la izquierda de \(x=1\) y decrece a su derecha, lo que implica que hay mínimos en \(x=0\) y \(x=2\).
Monotonía:
El signo de la primera derivada depende del numerador (el denominador siempre es positivo). Es fácil ver que la función es creciente a la izquierda de \(x=1\) y decreciente a su derecha.
Estos dos mínimos son absolutos porque la función es acotada y tienen el mismo valor:
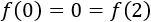
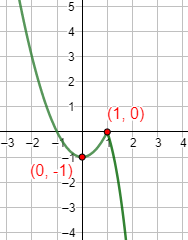
Gráfica:
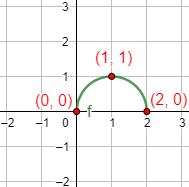
Función 9
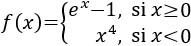
Solución
Dominio:
El dominio de la función es el conjunto de los reales.
Extremos:
Calculamos la derivada:
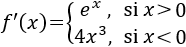
Calculamos los puntos críticos:
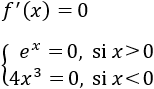
No hay puntos críticos. El único candidato a extremo es donde cambia la definición de la función: \(x=0\).
Para saber si es un extremo, estudiamos la monotonía alrededor del punto.
Monotonía:
Estudiamos el signo de la derivada:
![la derivada es negativa en ]-∞,0[ y positiva en ]0,+∞[ Recordamos los conceptos de extremos relativos y absolutos (máximos y mínimo) y los criterios de la primera y la segunda derivada. Resolvemos 20 problemas de aplicación. Extremos de funciones. Matemáticas. Cálculo diferencial.](https://www.matesfacil.com/BAC/extremos/F9-3.png)
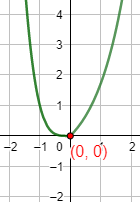
La función decrece en los negativos y crece en los positivos. Por tanto, tiene un mínimo absoluto en \(x=0\).
Gráfica:
Función 10
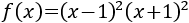
Solución
Dominio:
El dominio es \(\mathbb{R}\).
Extremos:
Desarrollamos los productos para calcular la derivada fácilmente:
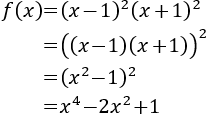
La derivada es
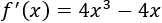
Buscamos los puntos críticos:
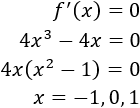
Calculamos la segunda derivada:
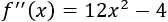
Evaluamos la segunda derivada en los puntos críticos:
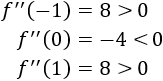
Por tanto, hay mínimos en \(x=-1\) y en \(x=1\) y un máximo en \(x=0\).
Monotonía:
Reescribimos la derivada para ver fácilmente su signo:
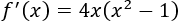
Es rápido ver que la función es decreciente, creciente, decreciente y creciente, respectivamente, en los intervalos
![intervalos ]-∞,-1[, ]-1,0[, ]0,1[, y ]1,+∞[ Recordamos los conceptos de extremos relativos y absolutos (máximos y mínimo) y los criterios de la primera y la segunda derivada. Resolvemos 20 problemas de aplicación. Extremos de funciones. Matemáticas. Cálculo diferencial.](https://www.matesfacil.com/BAC/extremos/F10-7.png)
Deducimos que al menos uno de los dos mínimos es absoluto. Calculamos la imagen de ambos para averiguarlo:
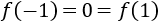
Como sus imágenes coinciden, ambos son absolutos.
Gráfica:
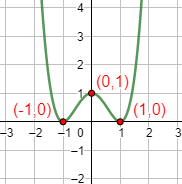
Función 11
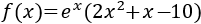
Solución
Dominio:
El dominio es \(\mathbb{R}\).
Extremos:
Calculamos la derivada:
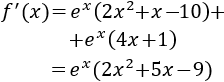
Calculamos los puntos críticos:
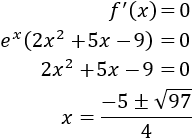
Calculamos la segunda derivada:
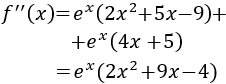
Evaluamos la segunda derivada en los puntos críticos:
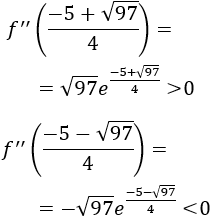
Monotonía:
Teniendo en cuenta el signo de la parábola \(2x^2+5x-9\), la función es creciente, decreciente y creciente, respectivamente, en los intervalos
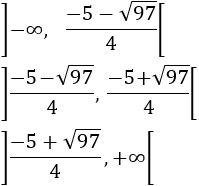
Deducimos que el mínimo es absoluto.
Gráfica:
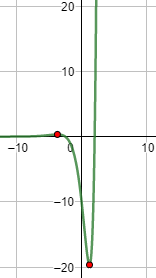
Función 12
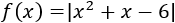
Solución
Dominio:
El dominio es el conjunto de los reales.
Extremos:
Vamos a reescribir la función como una función a trozos. Para ello, buscamos los intervalos en los que cambia el argumento del valor absoluto:
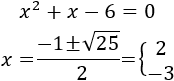
Damos valores a \(x\) para determinar el signo del polinomio:
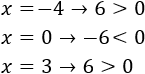
Por tanto, podemos escribir la función como
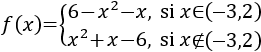
Calculamos la derivada:
![f'(x) = -2x-1 si x pertenece a (-3,2) y f'(x) = 2x+1 si x no pertenece a [-3,2] Recordamos los conceptos de extremos relativos y absolutos (máximos y mínimo) y los criterios de la primera y la segunda derivada. Resolvemos 20 problemas de aplicación. Extremos de funciones. Matemáticas. Cálculo diferencial.](https://www.matesfacil.com/BAC/extremos/F12-4.png)
Calculamos los puntos críticos:
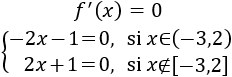
El único punto crítico es \(x = -1/2\).
Calculamos la segunda derivada:
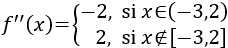
Evaluamos la segunda derivada en el punto crítico:
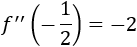
Como es negativa, se trata de un máximo.
Monotonía:
Estudiamos el signo de la derivada:
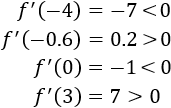
La función es decreciente, creciente, decreciente y creciente, respectivamente, en los intervalos
![intervalos ]-∞,-3[, ]-3,-1/2[, ]-1/2,2[ y ]2,+∞[, Recordamos los conceptos de extremos relativos y absolutos (máximos y mínimo) y los criterios de la primera y la segunda derivada. Resolvemos 20 problemas de aplicación. Extremos de funciones. Matemáticas. Cálculo diferencial.](https://www.matesfacil.com/BAC/extremos/F12-9.png)
Por tanto, tiene mínimos en \(x = -3\) y en \(x = 2\).
El máximo no es absoluto porque la función tiende a infinito cuando \(x\to\pm\infty\).
Las imágenes de los mínimos son
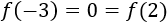
Luego ambos mínimos son absolutos.
Gráfica:
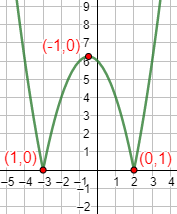
Función 13
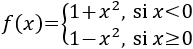
Solución
Dominio:
El dominio es \(\mathbb{R}\).
Extremos:
Calculamos la derivada:
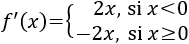
El único punto crítico es \(x=0\).
A continuación, vamos a ver que puede haber problemas cuando un punto crítico coincide con el punto donde cambia la definición de la función.
La derivada segunda es
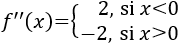
Observad que el segundo signo es estricto porque no podemos evaluar la segunda derivada en \(x=0\). Esto se debe a que la derivada se define como un límite y, en este caso, dicho límite no existe (los límites laterales son distintos):
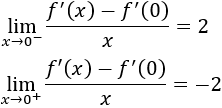
Podemos solventar este problema simplemente observando la monotonía de la función.
Monotonía:
Atendiendo al signo de la primera derivada, la función es decreciente en \(x<0\) y en \(x> 0\). Por tanto, \(x=0\) no es un extremo.
En realidad, el punto \(x=0\) es un punto de inflexión porque la función es convexa en \(x< 0\) y cóncava en \(x>0\) (esto lo sabemos por el signo del coeficiente principal de las parábolas que componen la función).
Gráfica:
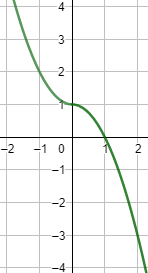
Función 14
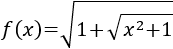
Solución
Dominio:
El dominio es el conjunto de los reales.
Extremos:
Calculamos la derivada:
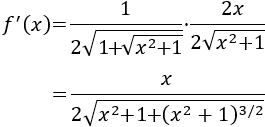
La derivada se anula en \(x=0\), así que éste es el único punto crítico.
Como el cálculo de la segunda derivada es tedioso, usaremos la monotonía de la función para saber si se trata de un máximo o de un mínimo.
Monotonía:
El signo de la derivada es negativo para \(x\) negativos y positivo para \(x\) positivos. Por tanto, la función es decreciente en los negativos y creciente en los positivos. Como consecuencia, \(x=0\) es un mínimo.
El extremo es absoluto porque la función tiende a infinito cuando \(x\to \pm \infty\).
Gráfica:
Función 15
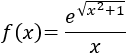
Solución
Dominio:
El dominio es \(\mathbb{R}\setminus\{0\}\).
Extremos:
Calculamos la derivada:
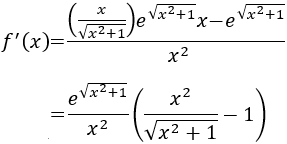
Calculamos los puntos críticos:
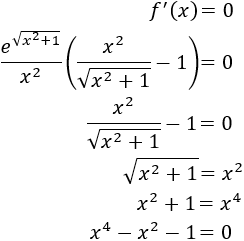
Tenemos una ecuación bicuadrada. Aplicando la fórmula cuadrática,
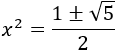
Descartamos la solución negativa, así que
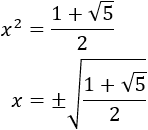
Como calcular la segunda derivada es tedioso, usaremos el criterio de la primera derivada para deducir los extremos.
Monotonía:
Para abreviar, escribiremos
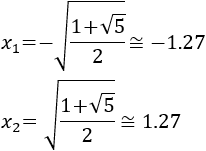
Tenemos que estudiar el signo de la derivada en los intervalos
![intervalos para estudiar el signo de la derivada: ]-∞,x1[, ]x1,0[, ]0,x2[ y ]x2,+∞[ Recordamos los conceptos de extremos relativos y absolutos (máximos y mínimo) y los criterios de la primera y la segunda derivada. Resolvemos 20 problemas de aplicación. Extremos de funciones. Matemáticas. Cálculo diferencial.](https://www.matesfacil.com/BAC/extremos/F15-6.png)
Observad que el signo de la derivada sólo depende del factor
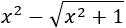
Damos valores a \(x\):
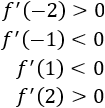
La función es creciente en el primer y cuarto intervalo y decreciente en los otros dos.
Por tanto, \(x_1\) es un máximo y \(x_2\) es un mínimo.
Los extremos no son absolutos porque la función no es acotada.
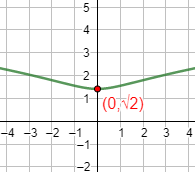
Gráfica:
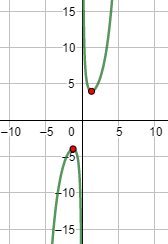
Función 16
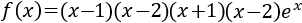
Solución
Dominio:
El dominio es \(\mathbb{R}\).
Extremos:
Para facilitar el cálculo de la derivada, reescribimos la función
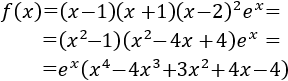
Calculamos la derivada:
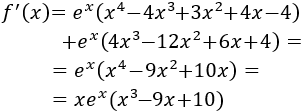
Calculamos los puntos críticos:
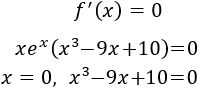
Aplicando Ruffini y resolviendo la ecuación de segundo grado que obtenemos, los puntos críticos son
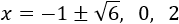
Calculamos la segunda derivada:
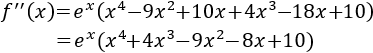
Evaluamos la segunda derivada en los puntos críticos:
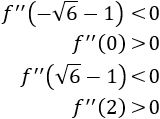
Por tanto, \(x = -1\pm \sqrt{6}\) son máximos y \(x=0\) y \(x=2\) son mínimos.
Los máximos no son absolutos ya que la función no está acotada superiormente:
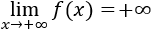
En cambio,
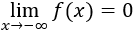
Así que alguno de los mínimos debe de ser absoluto.
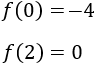
Luego \(x=0\) es un mínimo absoluto.
Gráfica:
Problema 1
Demostrar la siguiente desigualdad:
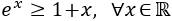
Solución
Sea la función
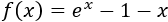
Su dominio es todo \(\mathbb{R}\).
Su derivada es
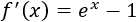
Buscamos los puntos críticos:
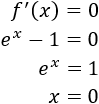
El único punto crítico es \(x=0\).
La segunda derivada es
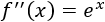
La evaluamos en \(x=0\):
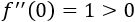
Luego \(x=0\) es un mínimo.
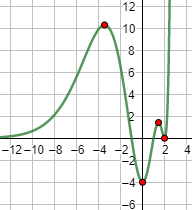
Teniendo en cuenta el signo de la derivada, la función es decreciente para \(x<0\) y creciente para \(x>0\). Así que el mínimo es absoluto.
Como \(f(0)=0\) y \(x=0\) es un mínimo, tenemos
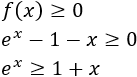
Gráficas:
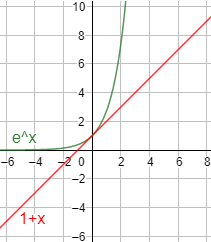
Problema 2
Resolver la siguiente inecuación:
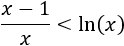
Solución
Sea la función
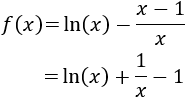
El dominio de la función es \((0,+\infty )\).
Calculamos la derivada:
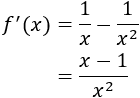
Sólo hay un punto crítico: \(x = 1\).
Teniendo en cuenta el signo de la derivada, la función es decreciente en \((0,1)\) y creciente \((1,+\infty)\). Por tanto, \(x = 1\) es un mínimo absoluto.
El mínimo de la función es \(f(1) =0\), por tanto,
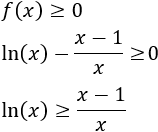
La igualdad se da cuando \(x=1\).
Por tanto, las soluciones de la inecuación son
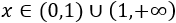
Gráficas:
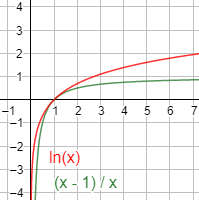
Problema 3
Demostrar que toda parábola tiene un extremo absoluto en \(x=-b/(2a)\).
Solución
Sea la función (\(a\neq 0\)) parabólica
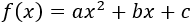
Su derivada es
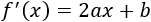
Su único punto crítico es
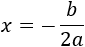
Su derivada segunda es
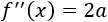
Por tanto, el punto crítico es un máximo si \(a<0\) y es un mínimo si \(a>0\).
Los límites de \(f(x)\) cuando \(x\to \pm \infty\) son infinitos (su signo depende del de \(a\)), así que los extremos son absolutos.
Problema 4
Demostrar que la siguiente función siempre tiene un máximo y un mínimo:
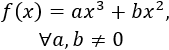
Solución
La derivada de la función es
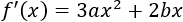
Calculamos los puntos críticos:
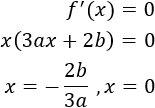
Calculamos la segunda derivada:
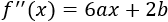
Evaluamos la segunda derivada en los puntos críticos:
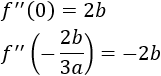
Independientemente de los valores de los parámetros, la segunda derivada en un punto crítico es positiva y en el otro es negativa. Por tanto, la función \(f\) tiene un máximo y un mínimo absolutos.


Cálculo de extremos de funciones - © matesfacil.com

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.

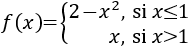
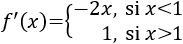
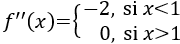
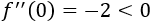
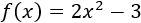
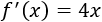
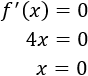
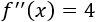
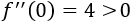
![signos negativo en ]-∞0[ y signo positivo en ]0,+∞[ Recordamos los conceptos de extremos relativos y absolutos (máximos y mínimo) y los criterios de la primera y la segunda derivada. Resolvemos 20 problemas de aplicación. Extremos de funciones. Matemáticas. Cálculo diferencial.](https://www.matesfacil.com/BAC/extremos/F1-5.png)

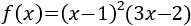
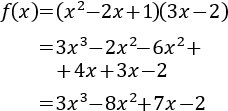
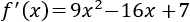
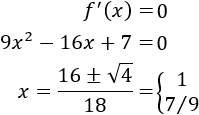
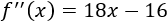
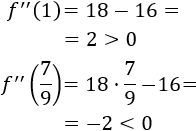
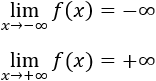

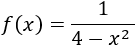
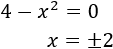
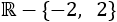
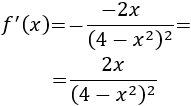
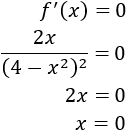
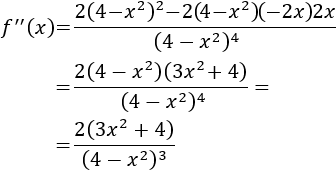
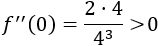
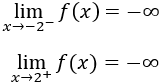
![]-∞,-2[ U ]-2,0[ U ]0,2[ U ]2,+∞[ Recordamos los conceptos de extremos relativos y absolutos (máximos y mínimo) y los criterios de la primera y la segunda derivada. Resolvemos 20 problemas de aplicación. Extremos de funciones. Matemáticas. Cálculo diferencial.](https://www.matesfacil.com/BAC/extremos/F3-8.png)
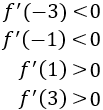

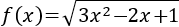
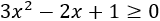
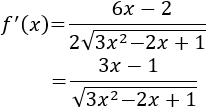
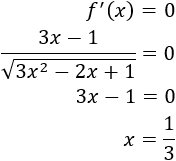
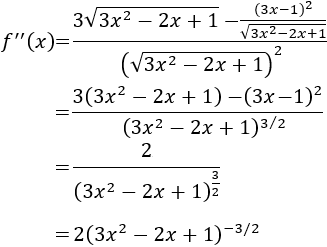
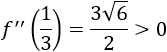
![la derivada es negativa en el intervalo ]-∞,1/3[ y es positiva en ]1/3,+∞[ Recordamos los conceptos de extremos relativos y absolutos (máximos y mínimo) y los criterios de la primera y la segunda derivada. Resolvemos 20 problemas de aplicación. Extremos de funciones. Matemáticas. Cálculo diferencial.](https://www.matesfacil.com/BAC/extremos/F4-6.png)

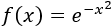
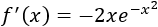
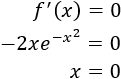
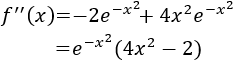
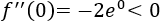
![la derivada es positiva en el intervalo ]-∞,0[ y negativa en ]0,+∞[ Recordamos los conceptos de extremos relativos y absolutos (máximos y mínimo) y los criterios de la primera y la segunda derivada. Resolvemos 20 problemas de aplicación. Extremos de funciones. Matemáticas. Cálculo diferencial.](https://www.matesfacil.com/BAC/extremos/F5-5.png)

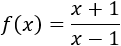
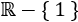
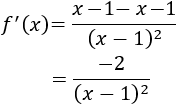
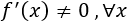

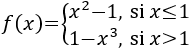
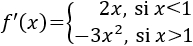
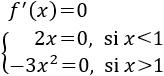
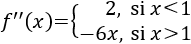
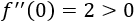
![derivada negativa en ]-∞,0[, positiva en ]0,1[ y negativa en ]1,+∞[ Recordamos los conceptos de extremos relativos y absolutos (máximos y mínimo) y los criterios de la primera y la segunda derivada. Resolvemos 20 problemas de aplicación. Extremos de funciones. Matemáticas. Cálculo diferencial.](https://www.matesfacil.com/BAC/extremos/F7-5.png)
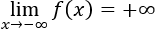

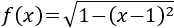
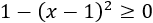
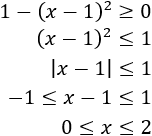
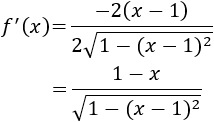
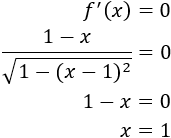
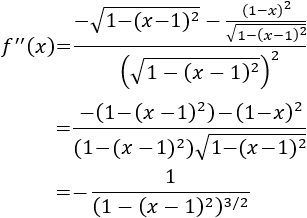
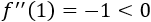
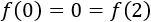

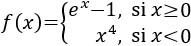
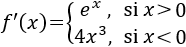
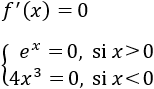
![la derivada es negativa en ]-∞,0[ y positiva en ]0,+∞[ Recordamos los conceptos de extremos relativos y absolutos (máximos y mínimo) y los criterios de la primera y la segunda derivada. Resolvemos 20 problemas de aplicación. Extremos de funciones. Matemáticas. Cálculo diferencial.](https://www.matesfacil.com/BAC/extremos/F9-3.png)

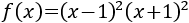
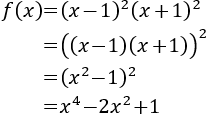
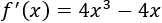
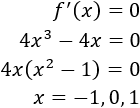
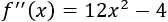
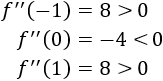
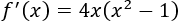
![intervalos ]-∞,-1[, ]-1,0[, ]0,1[, y ]1,+∞[ Recordamos los conceptos de extremos relativos y absolutos (máximos y mínimo) y los criterios de la primera y la segunda derivada. Resolvemos 20 problemas de aplicación. Extremos de funciones. Matemáticas. Cálculo diferencial.](https://www.matesfacil.com/BAC/extremos/F10-7.png)
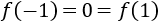

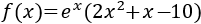
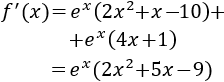
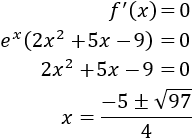
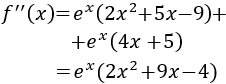
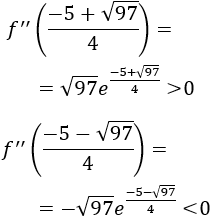
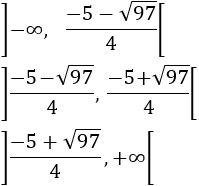

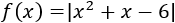
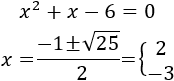
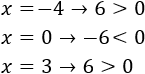
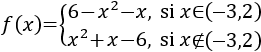
![f'(x) = -2x-1 si x pertenece a (-3,2) y f'(x) = 2x+1 si x no pertenece a [-3,2] Recordamos los conceptos de extremos relativos y absolutos (máximos y mínimo) y los criterios de la primera y la segunda derivada. Resolvemos 20 problemas de aplicación. Extremos de funciones. Matemáticas. Cálculo diferencial.](https://www.matesfacil.com/BAC/extremos/F12-4.png)
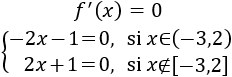
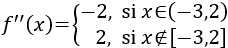
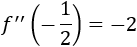
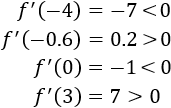
![intervalos ]-∞,-3[, ]-3,-1/2[, ]-1/2,2[ y ]2,+∞[, Recordamos los conceptos de extremos relativos y absolutos (máximos y mínimo) y los criterios de la primera y la segunda derivada. Resolvemos 20 problemas de aplicación. Extremos de funciones. Matemáticas. Cálculo diferencial.](https://www.matesfacil.com/BAC/extremos/F12-9.png)
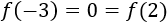

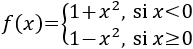
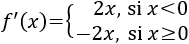
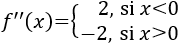
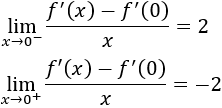

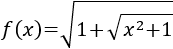
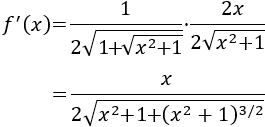

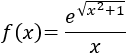
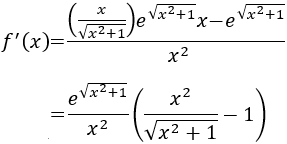
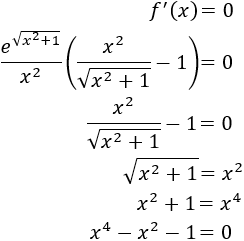
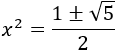
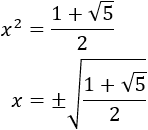
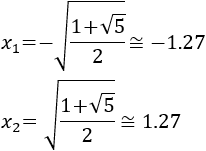
![intervalos para estudiar el signo de la derivada: ]-∞,x1[, ]x1,0[, ]0,x2[ y ]x2,+∞[ Recordamos los conceptos de extremos relativos y absolutos (máximos y mínimo) y los criterios de la primera y la segunda derivada. Resolvemos 20 problemas de aplicación. Extremos de funciones. Matemáticas. Cálculo diferencial.](https://www.matesfacil.com/BAC/extremos/F15-6.png)