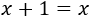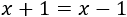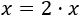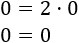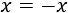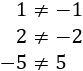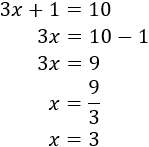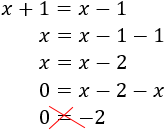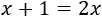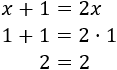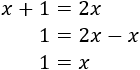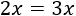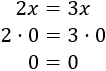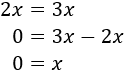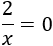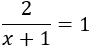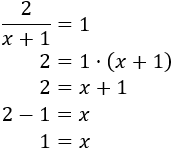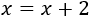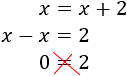¿Todas las ecuaciones tienen solución?

En esta página resolvemos una típica pregunta que suele surgir a los estudiantes cuando aprenden a resolver ecuaciones: ¿todas las ecuaciones tienen solución? La respuesta corta es que no:

Para comprender esta respuesta, vamos a recordar algunos conceptos y ver algunos ejemplos.

Contenido de esta página:

1. Concepto de ecuación y solución
2. Traducción de la ecuación
3. Ecuaciones sin solución
4. Ecuaciones engañosas
5. ¿Cómo saber si hay solución?
6. Problemas resueltos

Una ecuación es una expresión matemática en la que aparece un signo igual (\(=\)) y al menos una incógnita (\(x\)). Por ejemplo,

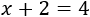
Resolver la ecuación consiste en encontrar el número o números que tiene que valer \(x\) para que la igualdad matemática sea cierta.

Por ejemplo, si cambiamos \(x\) por 3, la igualdad no se cumple:

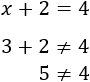
Nota: el signo \(\neq\) significa "no igual que" o "distinto que".

Sin embargo, si cambiamos \(x\) por \(2\), la igualdad sí se cumple:

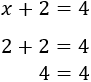
Resolver una ecuación es un proceso en el que se realizan operaciones matemáticas para averiguar cuál es la o las soluciones de la ecuación, es decir, encontrar el número que debe valer \(x\) para que se cumpla la igualdad.

Las ecuaciones pueden verse como una forma de expresar las propiedades de un número desconocido (\(x\)). Siguiendo con el ejemplo anterior, podemos traducir la ecuación \( x+2 = 4\) como

¿qué número da 4 cuando se le suma 2?

De este modo, es fácil ver que la solución de la ecuación es 2, porque 2 más 2 es igual a 4.

Como segundo ejemplo, la traducción de la ecuación \(x-1 =0\) podría ser

¿qué número da 0 cuando se le resta 1?

Es obvio que la solución de esta ecuación es 1 ya que 1 menos 1 es igual a 0.

Esta traducción de las ecuaciones nos ayudará a comprender cuándo una ecuación no tiene solución, como veremos en el siguiente apartado.

Comencemos por un ejemplo sencillo de ecuación sin solución:

La traducción de esta ecuación podría ser

¿qué número es igual a sí mismo cuando se le suma 1?

Ningún número es igual a sí mismo después de sumarle 1. Por tanto, esta ecuación no tiene solución.

Segundo ejemplo:

La siguiente ecuación tampoco tiene solución:

La traducción podría ser

¿qué número da el mismo resultado si le sumas 1 que si le restas 1?

La respuesta es ninguno, porque si sumamos 1 a \(x\), obtenemos un número mayor que \(x\), y si restamos 1 a \(x\), obtenemos un número menor que \(x\). Lógicamente, un número mayor que \(x\) no puede ser menor que \(x\).

Algunas ecuaciones parecen no tener solución a priori, lo que significa que debemos ser cautelosos a la hora de decidir si la ecuación tiene o no solución. Veamos un sencillo ejemplo:

Una posible traducción de esta ecuación es

¿qué número es igual a su doble?

Si pensamos en números naturales como 1, 2 y 3, sabemos que no son iguales a sus dobles, que son 2, 4 y 6, respectivamente. Sin embargo, no debemos olvidar el 0, que sí es igual a su doble:

Otra ecuación similar a la anterior es

Lógicamente, los números distintos de 0 no pueden ser iguales a sus opuestos:

Pero, al igual que antes, la solución de esta ecuación es 0.

Visto ya que una ecuación puede tener o no solución, la cuestión que surge ahora es cómo saber si una ecuación tiene solución. Desde luego, la mejor manera de saber si una ecuación tiene solución es hallarla. Si esto no es posible, entonces la ecuación no tiene solución.

En la página resolución de ecuaciones explicamos cómo resolver ecuaciones lineales (ecuaciones de primer grado), que son las más sencillas de resolver. Resumiendo, para resolver la ecuación operamos en ella moviendo los sumandos de un lado a otro de la igualdad y simplificando.

Veamos como ejemplo cómo resolver la ecuación \(3x +1 = 10\):

Para resolverla, hemos pasado el 1 de la izquierda restando al otro lado y el 3 lo hemos pasado dividiendo.

Tomemos como ejemplo una de las ecuaciones anteriores sin solución e intentemos resolverla:

Hemos llegado a la igualdad \(0=-2\), la cual es falsa. Esto nos dice que la ecuación no tiene solución. La explicación de esto es sencilla:

Todas las ecuaciones escritas a partir de una de ellas son equivalentes entre sí (es decir, son iguales). Por tanto, sea cual sea el valor que le demos a \(x\), se obtendrá una igualdad falsa, como la última, así que no existe ningún número que haga cumplir la igualdad de la ecuación (es decir, no existe solución).

Problema 1

¿La siguiente ecuación tiene solución?

Problema 2

¿La siguiente ecuación tiene solución?

Problema 3

¿La siguiente ecuación tiene solución?

Problema 4

¿La siguiente ecuación tiene solución?

Problema 5

¿La siguiente ecuación tiene solución?