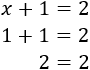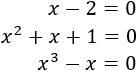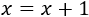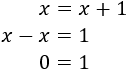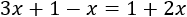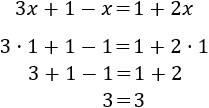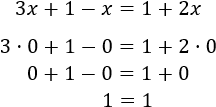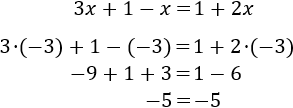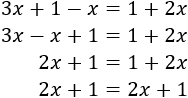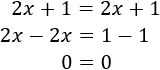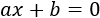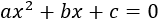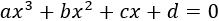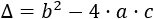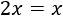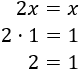¿Cuántas soluciones tiene una ecuación?
En la página ¿todas las ecuaciones tienen solución? explicamos que una ecuación puede tener o no solución, pero en esta página nos preguntamos ¿cuántas soluciones tiene una ecuación?
Para contestar a esta pregunta, recordamos algunos conceptos y proporcionamos varios ejemplos que nos ayuden a comprender. No obstante, adelantamos una respuesta genérica:
El número de soluciones de una ecuación depende del tipo de ecuación.
Nota: para facilitar la comprensión, nos centraremos en las ecuaciones polinómicas.
Contenido de esta página:
- Ecuación, incógnita y solución
- Tipo de ecuación
- Ecuación sin solución
- Ecuación con infinitas soluciones
- Ecuaciones polinómicas
- Ecuaciones polinómicas (2)
- Problemas resueltos
Páginas relacionadas
Ecuaciones por niveles:
Otras páginas:
1. Ecuación, incógnita y solución
De forma abreviada, recordamos que una ecuación es una igualdad entre dos expresiones matemáticas en las cuales aparece una o varias incógnitas (normalmente, \(x\)). La incógnita representa el número desconocido que hace que la igualdad sea cierta, el cual se desea hallar. A dicho número se le llama solución.
Consideremos la siguiente ecuación:
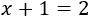
El número que debe valer \(x\) para que la igualdad anterior sea cierta es \(1\), puesto que 1 más 1 es igual a 2. Por tanto, la solución de dicha ecuación es \(x=1\).
Comprobamos que \(x=1\) verifica la ecuación: