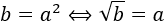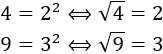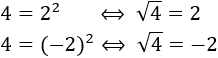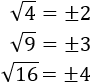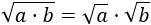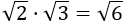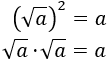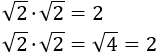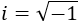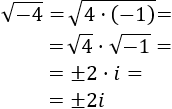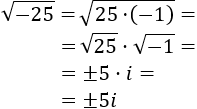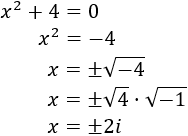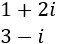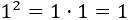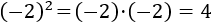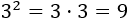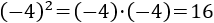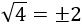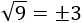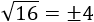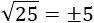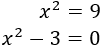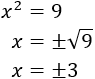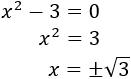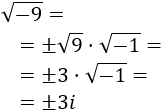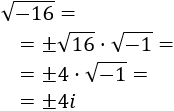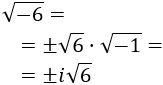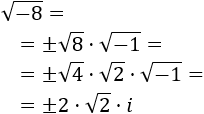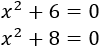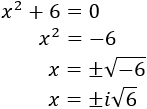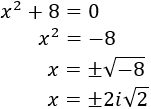¿Existe la raíz cuadrada de un número negativo?

En esta página resolvemos la pregunta ¿existe la raíz cuadrada de un número negativo? La respuesta es que sí a pesar de que, en teoría, el cuadrado de un número no puede ser negativo. Para poder comprender la existencia de las raíces de negativos, recordaremos algunos conceptos y propiedades de las potencias y raíces, llegando finalmente a la definición de los números imaginarios. También, resolvemos algunos problemas.

Contenido de esta página:

1. Cuadrado de un número
2. Raíz cuadrada de un número
3. Producto de raíces
4. Raíz cuadrada de un negativo
5. Ecuaciones de segundo grado
6. Alusión a los complejos
7. Problemas resueltos

El cuadrado de un número \(a\) es

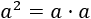
El número \(a^2\) se dice que es una potencia de base \(a\) y exponente 2.

Por ejemplo, calculamos el cuadrado de 2 y de 3:

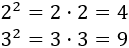
Si la base es un número negativo, debemos escribir la potencia con paréntesis:

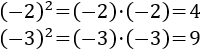
Nota: recordad que el producto de dos números negativos es positivo (regla de los signos).

Si no escribimos el paréntesis, el signo queda fuera de la potencia:

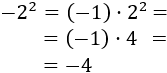
Hemos aprendido que, en teoría,

Y esto es lo mismo que decir

Sin embargo, esto no tiene por qué ser así, como veremos a continuación.

Nota: no es correcto decir que el cuadrado de un número siempre es positivo puesto que el cuadrado de 0 es 0 y no es positivo.

La raíz cuadrada del número \(b\) se denota por \(\sqrt{b}\) y es el número \(a\) tal que \(a^2 = b\). Es decir,

Por ejemplo,

Ahora bien, hay que tener en cuenta que, en realidad, un número tiene 2 raíces cuadradas.

Por ejemplo, las raíces cuadradas de 4 son 2 y -2:

Por esta razón, cuando calculamos la raíz cuadrada de un número, tenemos que escribir el signo \(\pm\):

No obstante, por comodidad, solemos omitir el signo \(\pm\), reservándolo para las ocasiones en que es absolutamente necesario.

Una importante propiedad de las raíces es la siguiente:

Es decir,

Por ejemplo,

Otra propiedad importante es que el cuadrado de la raíz cuadrada de un número es dicho número:

Por ejemplo,

En teoría, no existe la raíz cuadrada de un número negativo porque ningún número al cuadrado es negativo. Sin embargo, esto supone un inconveniente para resolver algunos problemas o ecuaciones matemáticas, por lo que se inventaron los números imaginarios.

La unidad imaginaria es \(i\) y se define como la raíz cuadrada de -1:

El cuadrado de la unidad imaginaria es -1:

Con la invención del número imaginario ya podemos trabajar con raíces cuadradas de números negativos (nos ayudaremos de la propiedad del producto de raíces).

Veamos algunos ejemplos:

• Raíces cuadradas de -4:

• Raíces cuadradas de -25:

Observad que, entonces, sí hay números cuyo cuadrado es negativo: los números imaginarios.

Por ejemplo,

Los números imaginarios, como números que son, se pueden sumar y restar:

Y, también, se pueden multiplicar y dividir:

Nota: hemos escrito \(i\) como una raíz y aplicado la propiedad del cuadrado de una raíz cuadrada.

Con los números imaginarios ya podemos resolver algunas ecuaciones de segundo grado cuyas soluciones son las raíces de números negativos.

Ejemplo 1: las soluciones de la ecuación \(x^2+1=0\) son \(x=i\) y \(x=-i\):

Ejemplo 2: las soluciones de la ecuación \(x^2+4=0\) son \(x=2i\) y \(x=-2i\):

Para no complicar demasiado estos conceptos, sólo diremos que existen unos números, los números complejos (\(\mathbb{C}\)), que están formados por una suma (o resta) de un número real y un número imaginario.

Ejemplos de números complejos:

Los números complejos se utilizan, por ejemplo, en la resolución de algunas ecuaciones de segundo grado.

Ejemplo: Las soluciones de la ecuación \(x^2 -2x + 2 = 0\) son los números complejos \(x = 1-i\) y \(x = 1+i\).

Los números complejos son un anillo dotado de suma y producto, \((\mathbb{C},+,·)\), y los números reales, \(\mathbb{R}\), son un subanillo de éstos.

Problema 1

Calcular el cuadrado de 1, -2, 3, y -4.

Problema 2

Calcular las raíces cuadradas de 4, 9, 16 y 25.

Problema 3

Resolver las siguientes ecuaciones:

Problema 4

Calcular las raíces cuadradas de -9 y -16.

Problema 5

Calcular las raíces cuadradas de -6 y -8.

Problema 6

Resolver las siguientes ecuaciones cuadráticas: